随机分布副本的方式被广泛引用到分布式领域。但是,随着集群规模的扩大,数据丢失的可能性直线上升。
通常情况下,分布式系统就会将自身服务进行分片,每个分片又会包含固定的副本数,然后将每个分片的副本随机分布在集群内。这里我们拿副本数为3的情况举例。每个分片会分布在不同的机器上,比如\(\{1,2,3\}\)、\(\{4,5,6\}\),随着分片的增多,这样的服务器排列组合也会随之增加。那么如果集群内任意挂掉3台服务器,那么导致任一分片的全部副本都损失的概率也随之增加。比如,最极端的例子,只要我们的副本使用的服务器的排列组合足够多,满足了任意3台服务器的全排列,则,集群内任意挂掉3台服务器时,必定会有一个分片的数据全部丢失。这个趋势,facebook的论文1中给出模拟图:
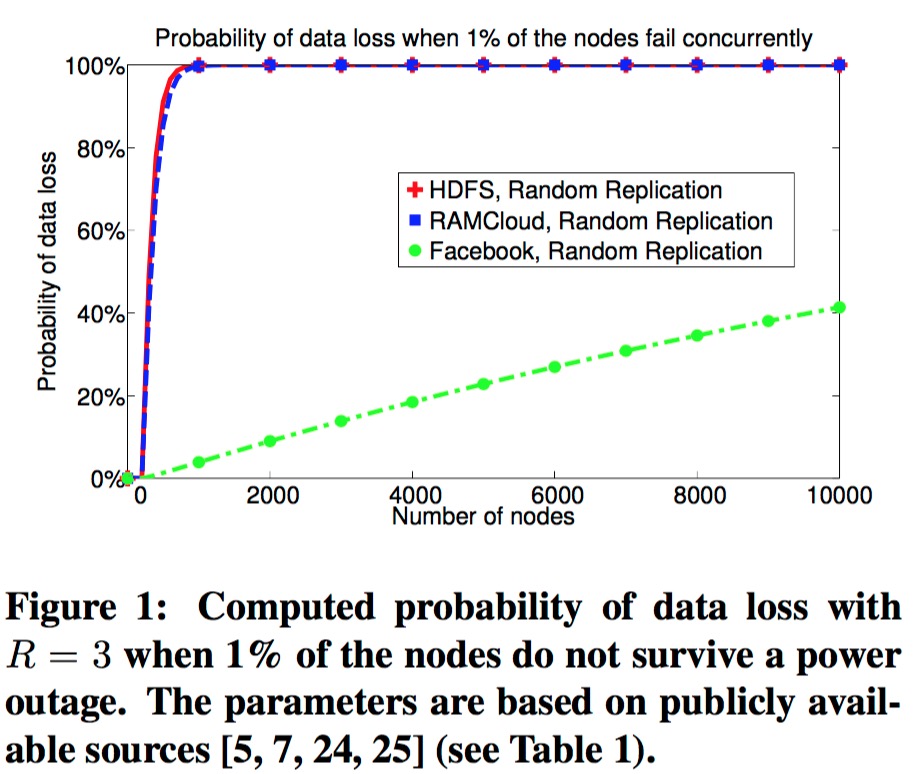
在以往的算法下,为了减少数据丢失的可能性,只能提升副本数,但是这样会带来成本的上升。 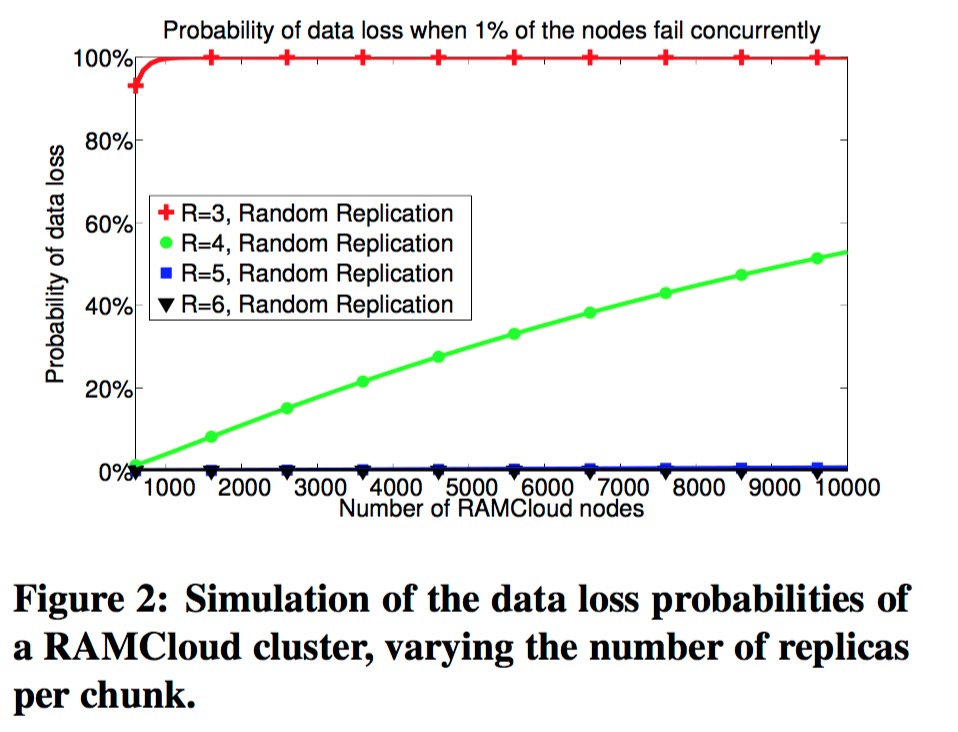
为了优化减少数据丢失的可能性,facebook提出了一种新的副本分布方式12,其将节点先划分为copyset。
为了解释论证,论文中首先提出了一个概念scatter width\(S\),\(S\)为在副本放置的组合中,任一节点与多少个其他节点有数据通信。比如我们的几个副本组合为\(\{1,2,3\}\),\(\{4,5,6\}\),\(\{7,8,9\}\),\(\{1,4,7\}\),\(\{2,5,8\}\),\(\{3,6,9\}\),则\(S = 4\),因为其中任一节点与其余4个节点有数据同步。比如6这个节点,它分别跟4,5,3,9同步数据。我们将一个分片的副本组合称为一个copyset,例如\(\{1,2,3\}\)为一个copyset。
- 如果副本分布的\(S\)太小,则故障恢复速度会慢,比如\(S\)为2,那个故障恢复时,只能从2个节点上恢复数据。
- 如果\(S\)太大,则会增加数据丢失的风险。因为当任意节点故障时,其波及的分片数随\(S\)的增大而增多。
故,论文中提出了4个核心变量:
- \(S\)
scatter width - \(R\) 副本数
- \(N\) 集群实例数
- \(P\) 副本排列组合次数
比如,我们有9个节点,当\(R = 3\)时,我们排列一次得,可选的副本分布为:\(\{1,2,3\}\),\(\{4,5,6\}\),\(\{7,8,9\}\),如果对应的分片数不够,则我们需要再排列一次,得到更多的副本组合,比如:\(\{1,4,7\}\),\(\{2,5,8\}\),\(\{3,6,9\}\)。
因此可得,\(S = P(R-1)\),copyset数为\(P\frac{N}{R}\),将\(S\)带入得\(\frac{S}{R-1} \cdot \frac{N}{R}\)。
论文中讲述,为了降低数据的丢失概率,排布数据副本时,追求更低的\(S\)。因为在实际情况中,故障恢复的瓶颈通常是服务器带宽,而不是\(S\)。
其算法可以简单描述为2个阶段:
- 排列阶段(
Permutation phase) - 选择副本阶段(
Replication phase)

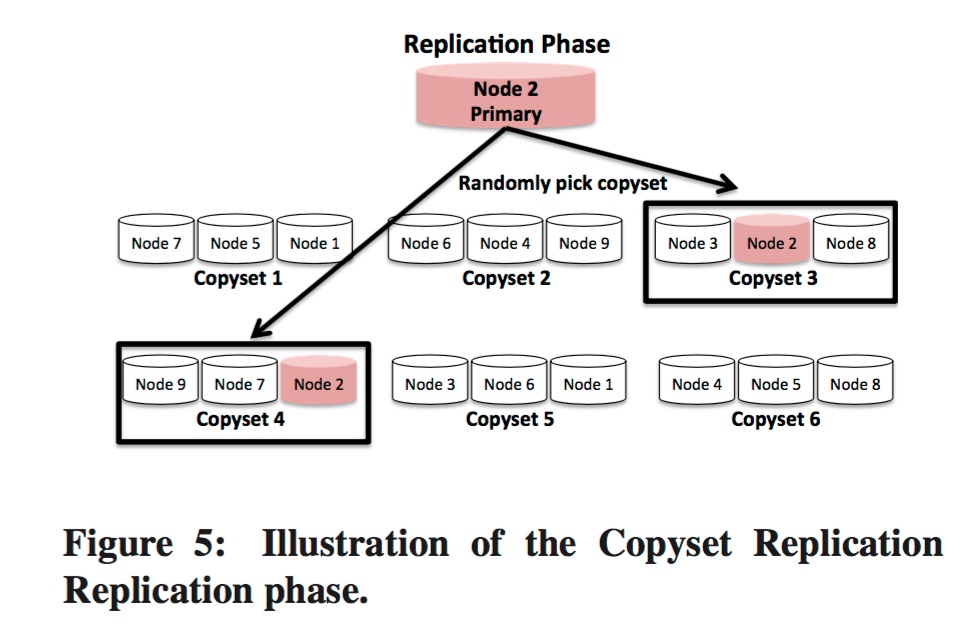
这2个阶段合起来简单描述为:
- 选定\(S\)和\(R\)
- 将集群实例排列\(P = \frac{S}{R-1}\)次,如果\(P\)不是一个整数,我们向上取整。
- 每次排列时,将集群节点完全随机排列,然后分为\(R\)组,每组为一个
copyset。在排列阶段,也可以加入一些约束条件,比如不要让相同机架的节点比邻等 - 选取任意集群节点为第一个/主副本,然后随机选取一个包含该节点的
copyset给对应的分片使用(上图中Replication phase中Node 2的箭头指向的copyset3和copyset4的含义为这2个copyset都满足条件,随机选取一个即可)
例如:一个集群有9个实例,我们需要一个3副本的且\(S = 2\)的分配方案,则我们需要排列\(P = \frac{2}{3-1}\)即1次。加入排列结果为:
[1, 6, 5, 3, 4, 8, 9, 7, 2]
然后我们将其分为3组
[1, 6, 5], [3, 4, 8], [9, 7, 2]
然后我们选择每组的第一个节点为主副本即可。
但是这个方法获得的结果不会总是最优解,比如\(S = 4\)时,我们可能得到如下结果:
[1, 6, 5], [3, 4, 8], [9, 7, 2]
[1, 2, 7], [5, 4, 6], [3, 9, 8]
我们可以看出,节点5的\(S\)只有3,我们可以重新再分配一次,或者直接接受这个结果,因为虽则集群节点数的增大,找到最优解的难度会很高。
论文中使用copyset算法后与之前的对比:
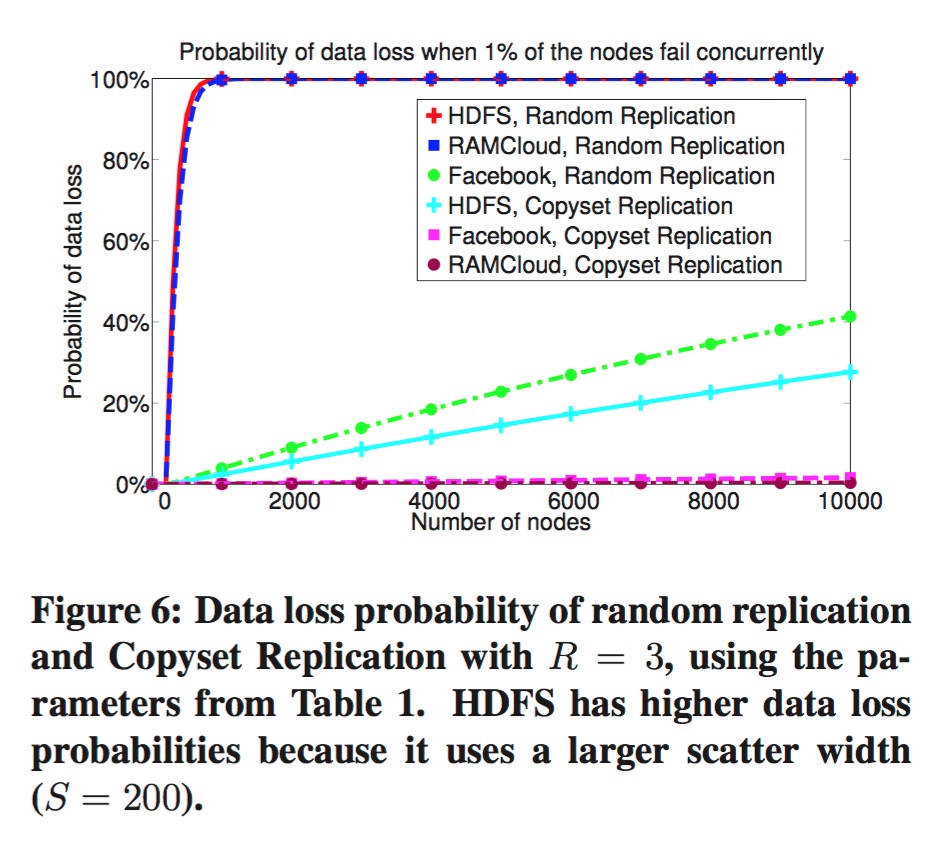
参考
文档信息
- 本文作者:Neal Hu
- 本文链接:https://lrita.github.io/2018/08/07/copysets-and-replications/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)