编：关于Vector Clock之前看过几眼，但是多数讲解地都不是很清楚，一直没太弄清楚。直到有一天，又看了看，终于弄明白了。

早在在1978年，Leslie Lamport就提出逻辑时钟的概念¹。在分布式环境中，通过一系列规则来定义逻辑时钟的变化。从而能通过逻辑时钟来对分布式系统中的事件的先后顺序进行判断。

逻辑时钟本质上定义了一种happen before关系，记作->，a->b意味着所有的进程都“认可”事件a发生在事件b之前。happen before关系满足传递性：即(a->b && b->c)可以推导出(a->c)。

Lamport’s Logical Clocks

lamport逻辑时钟算法：

• 每个事件对应一个Lamport时间戳，初始值为0
• 如果事件在节点内发生，时间戳加1
• 如果事件属于发送事件，时间戳加1并在消息中带上该时间戳
• 如果事件属于接收事件，时间戳 = Max(本地时间戳，消息中的时间戳) + 1

三个机器上各自跑着一个进程，分别为\(P_1\)，\(P_2\)，\(P_3\)，由于不同的机器上的物理时钟、CPU负载、或者CPU频率不一样，所以不同的机器上的时钟速率可能是不同的，例如当\(P_1\)所在的机器tick了6次，\(P_2\)所在的机器tick了8次，就是异步网络²中指的漂移时钟不同。

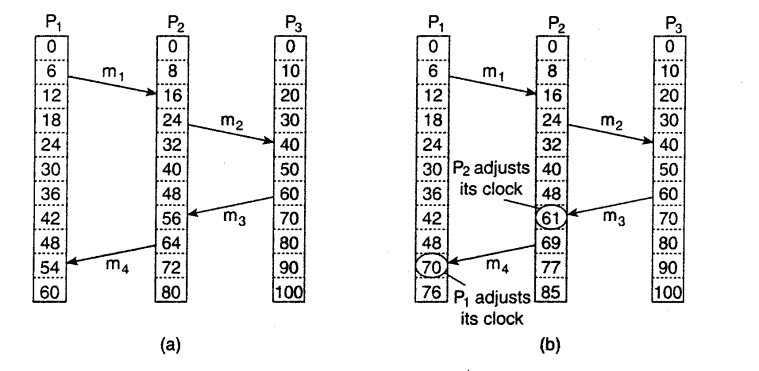
图中，\(P_1\)给\(P_2\)发送了消息\(m_1\)，\(m_1\)上附带了发送\(m_1\)时的时钟6，随后\(P_2\)收到了\(m_1\)，根据\(P_2\)接收到\(m_1\)时的时钟，认为传输消息花了16-6=10个tick，随后，\(P_3\)给\(P_2\)发送消息\(m_3\)，\(m_3\)附带的发送时钟是60。由于\(P_2\)的时钟走的比\(P_3\)的慢，所以接收到\(m_3\)时，本机的时钟56比发送时钟60小，这是不合理的，需要调整时钟，如图中，将\(P_2\)的56调整为61，即\(m_3\)的发送时钟加1。

当不同事件在不同进程间并行时³：

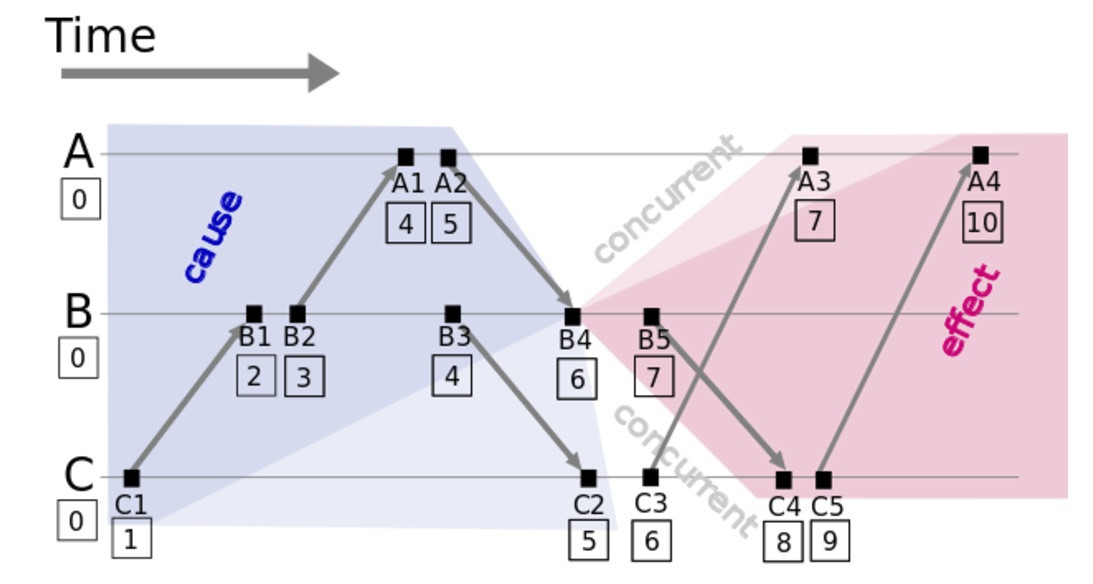
我们以B4事件为中心，来分析：

• 左侧深灰色的区域，我们根据happens before的传递性，很容易得出结论，他们都发生在B4之前，就是因果性中的“因(cause)”；
• 右侧深红色区域，我们也容易得出结论，他们都发生在B4之后，就是因果性中的“果(effect)”；
• 白色区域，是跟B4无关的事件，可以认为是并发关系；
• 但是在浅灰色和浅红色区域，其中的C2、A3两个事件与B4其实是并行关系，但是根据lamport逻辑时钟的逻辑，将他们判定为与B4具前后关系。可见lamport逻辑时钟并不能很好的表示并行关系。

lamport逻辑时钟规定：按事件的时间戳大小为时间排序，任何两个时间不可能在同一时间发生，任何消息收到的时间都应该比发送的时间晚。

Vector Clock

Vector Clock是在Lamport时间戳基础上演进的另一种逻辑时钟方法，它通过vector结构不但记录本节点的Lamport时间戳，同时也记录了其他节点的Lamport时间戳。Vector Clock的原理与Lamport时间戳类似，使用原理如下：

• 本地Vector Clock中每一个槽\(V[P_i]\)记录系统中对应进程\(P_i\)的逻辑时间戳；
• 初始化Vector Clock中每一个槽为0；
• 每一次处理内完内部事件，将本地的Vector Clock中自己槽中的逻辑时间戳+1；
• 每一次发送一个消息的时候，需要将本地的Vector Clock和消息一起发送；
• 每一次接收到一个消息的时候，需要将本地的Vector Clock中自己槽中的逻辑时间戳+1，同时更新本地的Vector Clock中每一个槽中的逻辑时间戳。\(V_{本地}[P_i] = MAX(V_{本地}[P_i], V_{消息}[P_i])\)

Vector Clock规定：

• \({事件}_i\)、\({事件}_j\)对应的Vector Clock中，每一个进程\(P_k\)的逻辑时间戳都满足\(V_i[P_k] < V_j[P_k]\)时，我们称\({事件}_i\)happen before\({事件}_j\)；
• 否则，即Vector Clock中，存在\(P_1\)、\(P_2\)，使得\(V_i[P_1] < V_j[P_1]，V_i[P_2] > V_j[P_2]\)，我们称\({事件}_i\)和\({事件}_j\)是并发关系(或者没有因果关系)；

因此在前面讲到的那个多进程并行时间的例子中³：

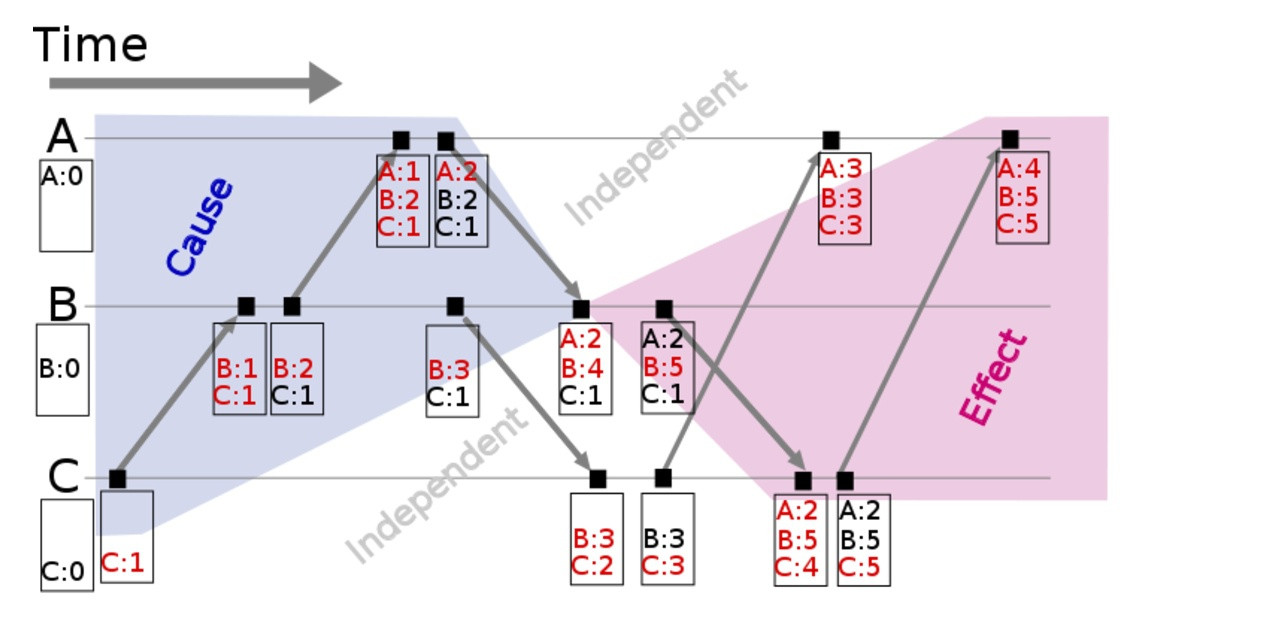
B4事件的Vector Clock为[A:2,B:4,C:1]，根据Vector Clock的规定，我们可以很好的判断出灰色区域happens beforeB4事件，B4时间happens before红色区域。白色区域与B4事件没有因果关系。

参考