注：本文中数学符号比较多，可能加载显示会比较慢。

基本概念

这里介绍的基本概念都是来自现代概率，建立在各种集合理论、测度论之上，与古典概率（\(\frac{期望结果}{全体结果}\)）在定义上有着许多不同。

样本空间

概率论中，样本空间是一个实验或随机试验所有可能结果的集合，而随机试验中的每个可能结果称为样本点。通常用\(S\)，\(\Omega\)或\(U\)表示。例如，如果抛掷一枚硬币，那么样本空间就是集合\(\{正面，反面\}\)。如果投掷一个骰子，那么样本空间就是\(\{1,2,3,4,5,6\}\)。

这个比较好理解，就是全体可能出现的结果的集合。

概率空间

概率空间\(( \Omega , F , P )\)是一个总测度为1的测度空间（即\(P ( \Omega ) = 1\)）.

第一项\(\Omega\)是一个非空集合，有时称作“样本空间”。\(\Omega\)的集合元素称作“样本输出”，可写作\(\omega\)。

第二项\(F\)是样本空间\(\Omega\)的幂集的一个非空子集。\(F\)的集合元素称为事件\(\sum\)。事件\(\sum\)是样本空间\(\Omega\)的子集。集合\(F\)必须是一个σ-代数：

1. \(\Phi \in \mathcal { F }\);
2. 若\(A \in \mathcal { F }\)，则\(\overline { A } \in \mathcal { F }\);
3. 若\(A _ { n } \in \mathcal { F } , \quad n = 1,2 , \ldots\),则\(\bigcup _ { n = 1 } ^ { \infty } A _ { n } \in \mathcal { F }\)

\(( \Omega , F )\)合起来称为可测空间。事件就是样本输出的集合，在此集合上可定义其概率。 第三项\(P\)称为概率，或者概率测度。这是一个从集合\(F\)到实数域\(R\)的函数，\(P : F \mapsto R\)。每个事件都被此函数赋予一个0和1之间的概率值。 概率测度经常以黑体表示，例如\(\mathbb { P }\)或\(\mathbb {Q}\)，也可用符号”Pr”来表示。

这段话是对概率空间的一个严格定义。我对这段话的理解是：

• \(\Omega\)试验中所有可能结果的集合（注：每个结果需要互斥，所有可能结果必须被穷举），因此\(P ( \Omega ) = 1\)，即事件的任一结果总会落入到\(\Omega\)中，比如投掷一个骰子，\(\Omega = \{1, 2, 3, 4, 5, 6\}\)。
• \(F\)是事件集合（即我们认为是“事件”的事件，我们想讨论的问题的集合），其中每个元素都是\(\Omega\)的子集，\(F\)中每个元素也是集合，可以穷举。并且它需要满足以下三点特性（也就是必须是σ-代数），至于为什么一定要满足σ-代数，原理性的东西不懂。比如投掷一个骰子，我们讨论的问题是“点数是偶数的概率”，则\(F = \{ \Phi, \{2, 4, 6\}, \{1, 3, 5\}\}\)。
• 概率\(P\)是定义在\(F\)上的一个函数，它的自变量是集合，该函数表示为\(\mathbb { P }\)或\(\mathbb {Q}\)，它将一个集合映射为一个实数。这是一个数学上的定义，概率是一个函数，表示一个随机过程，而实际生活中口头上的概率是一个实数，表示的具体事件发生的可能性。

随机变量

给定样本空间\(( S , \mathbb { F } )\) ，如果其上的实值函数\(X : S \rightarrow \mathbb { R }\)是\(\mathbb{F}\)(实值)可测函数，则称\(X\)为（实值）随机变量。初等概率论中通常不涉及到可测性的概念，而直接把任何\(X : S \rightarrow \mathbb { R }\)的函数称为随机变量。

如果\(X\)指定给概率空间\(S\)中每一个事件\(e\)有一个实数\(X ( e )\)，同时针对每一个实数\(r\)都有一个事件集合\(A_{r}\)与其相对应，其中\(A _ { r } = \{ e : X ( e ) \leqslant r \}\)，那么\(X\)被称作随机变量。随机变量一般用大写拉丁字母或小写希腊字母（比如\(X , Y , Z , \xi , \eta\)）来表示，从上面的定义注意到，随机变量实质上是函数，不能把它的定义与变量的定义相混淆，另外概率函数\(P\)并没有在考虑之中。

例如，随机掷两个骰子，整个事件空间可以由36个元素组成：
\(S = \{ ( i , j ) | i = 1 , \ldots , 6 , ; j = 1 , \ldots , 6 \}\)
这里可以构成多个随机变量，比如随机变量\(X\)（获得的两个骰子的点数和）或者随机变量\(Y\)（获得的两个骰子的点数差），随机变量\(X\)可以有11个整数值，而随机变量\(Y\)只有6个。
\(X ( i , j ) : = i + j , x = 2,3 , \dots , 12\)
\(Y ( i , j ) : = | i - j | , y = 0,1,2,3,4,5\)
又比如，在一次扔硬币事件中，如果把获得的背面的次数作为随机变量\(X\)，则\(X\)可以取两个值，分别是0和1。

概率分布

概率分布是概率论的一个概念。使用时可以有以下两种含义：

广义地，它指称随机变量的概率性质－－当我们说概率空间\(( \Omega , F , P )\)中的两个随机变量\(X\)和\(Y\)具有同样的分布（或同分布）时，我们是无法用概率\(\mathbb { P }\)来区别他们的。换言之：称\(X\)和\(Y\)为同分布的随机变量，当且仅当对任意事件\(A \in \mathcal { F }\)，有\(\mathbb { P } ( X \in A ) = \mathbb { P } ( Y \in A )\)成立。但是，不能认为同分布的随机变量是相同的随机变量。用更简要的语言来说，同分布是一种等价关系，每一个等价类就是一个分布。需注意的是，通常谈到的离散分布、均匀分布、伯努利分布、正态分布、泊松分布等，都是指各种类型的分布，而不能视作一个分布。

根据归类，抽象出了76种单变量概率分布，其中19种离散模型（矩形表示）和57种连续模型（圆角矩形表示）¹。

二项分布

二项分布是n个独立的“是/非”试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次”成功/失败”试验又称为伯努利试验。实际上，当n = 1时，二项分布就是伯努利分布。二项分布是显著性差异的二项试验的基础。

在每次试验中只有两种可能的结果，而且是互相对立的，且每次实验是独立的，与其它各次试验结果无关，结果事件发生的概率在整个系列试验中保持不变，则这一系列试验称为伯努利实验。比较常见的模型有：掷硬币、轮盘赌等。

当伯努利实验重复n次时，其概率分布为二项分布。

一般地，如果随机变量\(X\)服从参数为\(n\)和\(p\)的二项分布，我们记\(X \sim b ( n , p )\)或\(X \sim B ( n , p )\)。n次试验中正好得到k次成功的概率由概率质量函数给出：

\(f ( k ; n , p ) = \operatorname { Pr } ( X = k ) = \left( \begin{array} { c } { n } \\ { k } \end{array} \right) p ^ { k } ( 1 - p ) ^ { n - k }\)
对于\(k = 0,1,2 , \dots , n\)其中\(\left( \begin{array} { l } { n } \\ { k } \end{array} \right) = \frac { n ! } { k ! ( n - k ) ! }\)

那么X的期望值为\(\mathrm { E } [ X ] = n p\)

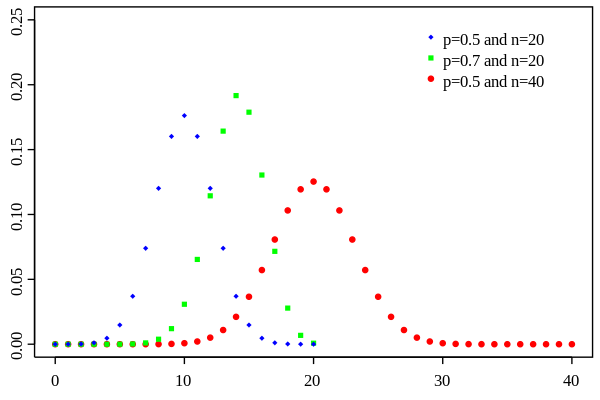
其概率质量函数图像为：

当n不变时，其函数图像特点为：p < 0.5时图形向左偏移；当 p > 0.5时，图形向右偏移。

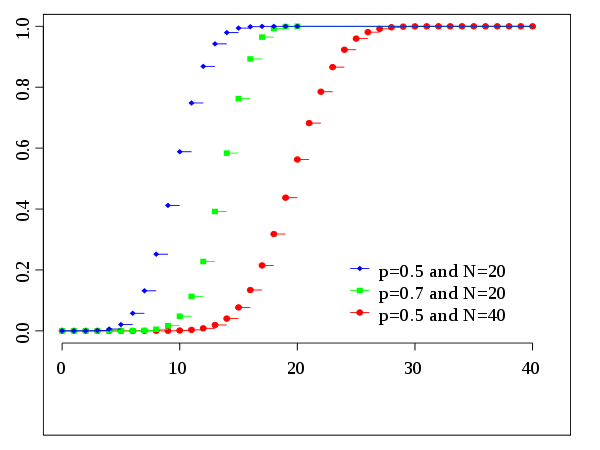
其概率累积函数图像为：

\[F ( x ; n , p ) = \operatorname { Pr } ( X \leq x ) = \sum _ { i = 0 } ^ { \lfloor x \rfloor } \left( \begin{array} { c } { n } \\ { i } \end{array} \right) p ^ { i } ( 1 - p ) ^ { n - i }\]

比如，红点组成的这条曲线，横轴代表试验成功的次数，纵轴代表该成功次数的概率。显而易见，当试验次数为40时，其概率在数学期望处（40*0.5）取得最大值，都成功、都失败的事件发生的概率处于最小值，这一点是很符合直觉的。

二项分布的应用

二项分布的数据收集比较容易，但是需要很大的样本量才能做出准确的评估。一些实际应用场景有：合格率抽检等。

在很多工厂里，通常都会跟零件供应商约定供货合格率，并对每批供货进行抽检，就是所谓的IQC。设约定的合格品率为97%，如果每批随机抽10件，那么抽出1件不合格时，整批的零件的合格率是不是达不到97%？

根据题意，p=0.97，n=10，k=9，据此算出10个样品中有9个合格品的概率是：

至于我们是否判定该批是否合格，那需要我们自己评判了。对于抽象检测这个问题，应该抽检多少样本、置信区间是多少，其实可以参考国标GB/T2828。

泊松分布

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布，而且每次实验是互相对立的，且每次实验是独立的。如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。

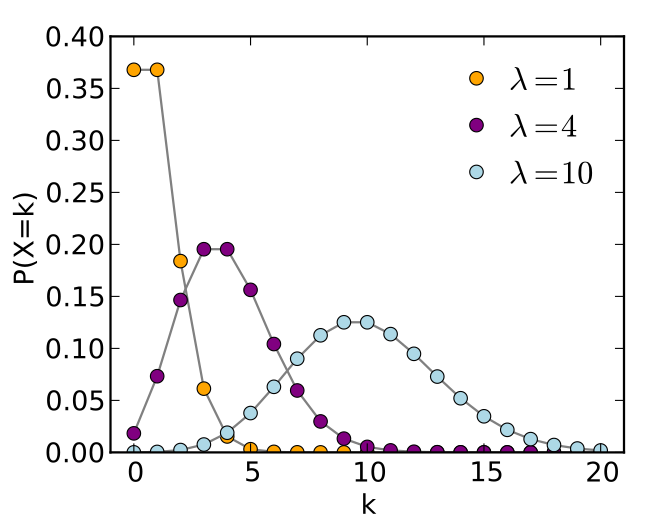
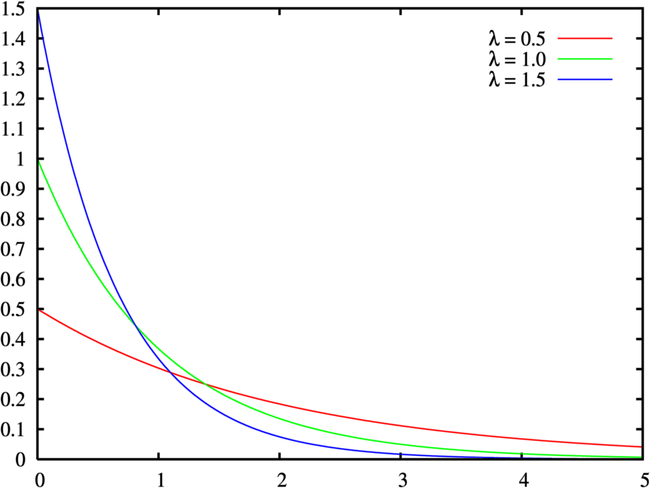
泊松分布的概率质量函数为：

\[P ( X = k ) = \frac { e ^ { - \lambda } \lambda ^ { k } } { k ! }\]

泊松分布的参数λ是单位时间（或单位面积）内随机事件的平均发生率。其数学期望是参数λ：E(X)=λ。

在二项分布的伯努利试验中，如果试验次数n很大，二项分布的概率p很小，λ比较稳定，且乘积λ = np比较适中（λ比较小导致np增长速度较慢或者存在有限值，经验法则是n≥20，p≤0.05）²，则事件出现的次数的概率可以用泊松分布来逼近。事实上，二项分布可以看作泊松分布在离散时间上的对应物。

其概率质量函数为：

其图像特点为，λ小时，分布向左偏斜；当λ大时，分布逐渐对称。

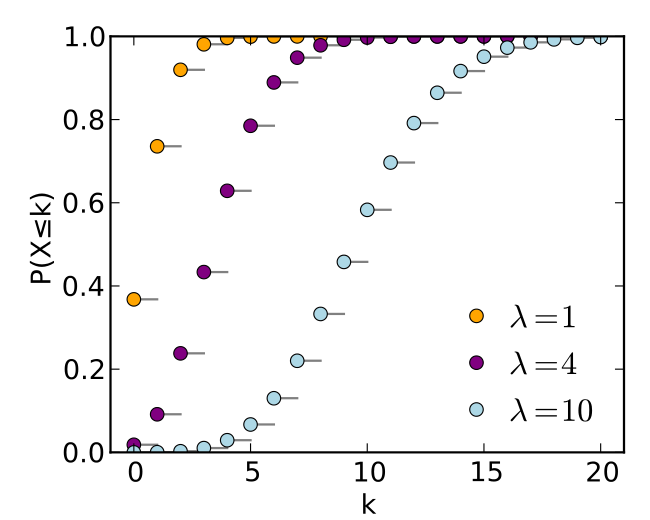
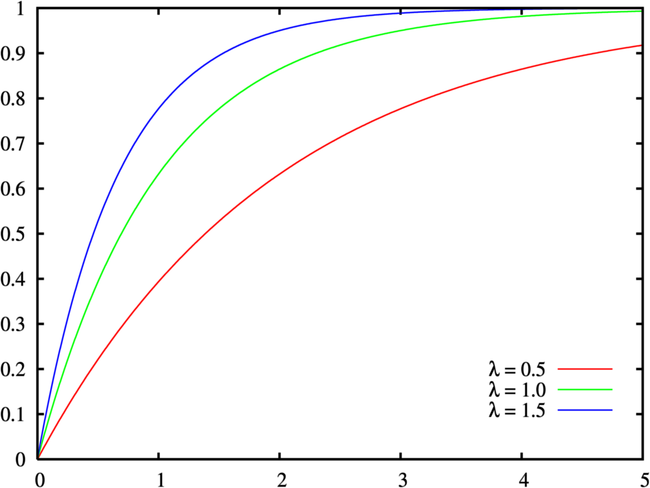
其概率累积函数为：

\[F(x; k, \lambda) = e ^ { - \lambda } \sum _ { i = 0 } ^ { \lfloor k \rfloor } \frac { \lambda ^ { i } } { i ! }\]

泊松分布有一个很好的性质，即如果把大区间分成若干个小区间，或者若干个小区间合并成1个大区间，则随机变量仍然服从泊松分布，其均值就变成为\(\frac { \lambda } {k}\)或\(\lambda \times k\)，其中\(k\)为分解或合并的区间数量。

当我们已知一个事件的概率分布为泊松分布时，我们可以通过对事件发生的频率来估计参数λ：
给定n个样本值ki，希望得到从中推测出总体的泊松分布参数λ的估计。为计算最大似然估计值，列出对数似然函数：

\(\begin{aligned} L ( \lambda ) & = \ln \prod _ { i = 1 } ^ { n } f \left( k _ { i } | \lambda \right) \\ & = \sum _ { i = 1 } ^ { n } \ln \left( \frac { e ^ { - \lambda } \lambda ^ { k _ { i } } } { k _ { i } ! } \right) \\ = & - n \lambda + \left( \sum _ { i = 1 } ^ { n } k _ { i } \right) \ln ( \lambda ) - \sum _ { i = 1 } ^ { n } \ln \left( k _ { i } ! \right) \\ \frac { \mathrm { d } } { \mathrm { d } \lambda } L ( \lambda ) = 0 & \Longleftrightarrow - n + \left( \sum _ { i = 1 } ^ { n } k _ { i } \right) \frac { 1 } { \lambda } = 0 \end{aligned}\)
解得λ从而得到一个驻点（stationary point）：

\[\widehat { \lambda } _ { \mathrm { MLE } } = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } k _ { i }\]

简单来说，我们估计一个泊松分布参数λ时，可以对该事件的频率进行多次采样，采样区间内的平均发生次数就是参数λ。例如，对某公共汽车站的客流做调查，统计了某天上午10:30到11:47来到候车的乘客情况。假定来到候车的乘客各批（每批可以是1人也可以是多人）是互相独立发生的。观察每20秒区间来到候车的乘客批次，共观察77分钟*3=231次，共得到230个观察记录。其中来到0批、1批、2批、3批、4批及4批以上的观察记录分别是100次、81次、34次、9次、6次。使用极大似然估计（MLE），得到λ的估计为（81*1+34*2+9*3+6*4）/231=0.8658。

泊松分布的应用

1. 假如经过长期观察统计，一个超市每天能卖出去3台电视，我们可以大致判定这个满足泊松分布，这样我们就可以用泊松分布来预测明天的电视销量，此时λ=3，明天卖出去0台、1台、2台、3台的概率分别是0.0498、0.1494、0.224、0.224。

2. 为保证设备的正常运行，必须配备一定数量的设备维修人员，现有同类设备300台，且各台设备工作相互独立，任一时刻发生故障的概率都是0.01，假设一台设备的故障由一人进行修理，问至少应配备多少名修理人员，才能保证设备发生故障后能得到及时修理的概率不小于0.99？

   根据描述，我们可以得知该机器故障分布符合泊松分布。总共有300台机器，故障概率0.01，则λ=300*0.01=3。为了保障每天机器都能够及时修理的概率大于0.99，则保证\(F(x; k, \lambda) > 0.99\)即可，为了简便，我们可以不求解此时\(k\)应该等于多少，我们可以使用一个循环，\(k\)从1开始累积，直到累积概率大于0.99，易得\(k\)至少为8，满足题意。

3. 来看泊松分布与美国枪击案中的一个例子。根据资料，1982–2012年枪击案的分布情况如下，能否判断美国治安正在恶化？

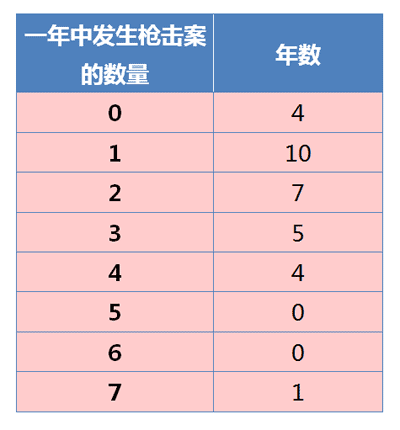
这里将该问题转化为：枪击案的统计是否满足泊松分布？如果满足泊松分布，则可以说明美国治安没有恶化，因为符合泊松分布的随机变量的发生概率是稳定的。反之则不能证明什么。

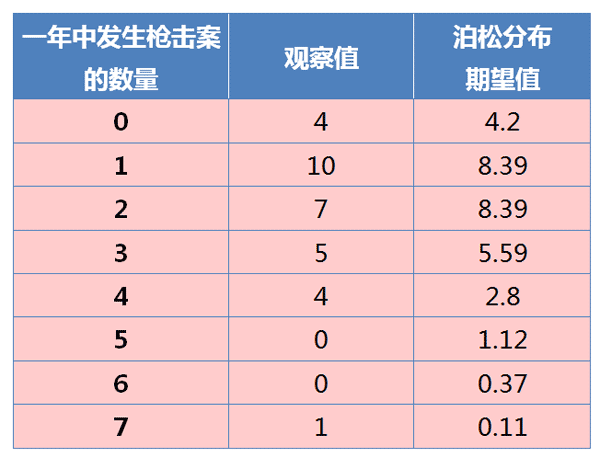
根据图中数据计算得到，平均每年发生2起枪击案，所以 λ = 2。然后拿样本分布和泊松分布进行比较：

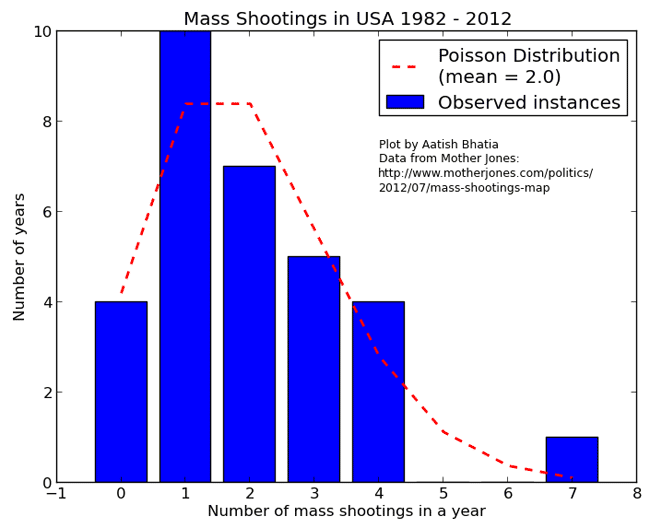
蓝色的条形柱是实际的观察值，红色的虚线是理论的预期值。可以看到，观察值与期望值还是相当接近的。

我们用卡方检验（chi-square test），检验观察值与期望值之间是否存在显著差异：

其中\(\overline { E } _ { i }\)是每个分类的期望值，\(v _ { i }\)是每个分类的观察值。

计算得到，卡方统计量等于9.82。查表后得到，置信水平0.90、自由度7的卡方分布临界值为12.017。因此，卡方统计量小于临界值，这表明枪击案的观察值与期望值之间没有显著差异。所以，可以接受”发生枪击案的概率是稳定的”假设，也就是说，从统计学上无法得到美国治安正在恶化的结论。但是，也必须看到，卡方统计量9.82离临界值很接近，p-value只有0.18。也就是说，对于”美国治安没有恶化”的结论，我们只有82%的把握，还有18%的可能是我们错了。

指数分布

指数分布（英语：Exponential distribution）是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔、中文维基百科新条目出现的时间间隔等等。

其概率密度函数为：

\[f ( x ; \lambda ) = \left\{ \begin{array} { c l } { \lambda e ^ { - \lambda x } } & { , x \geq 0 } \\ { 0 } & { , x < 0 } \end{array} \right.\]

从函数图像上比较好理解，当事件发生频率比较固定时，间隔时间越短的期望越高。因为直觉上，下一次事件不会马上发生。

其中λ > 0是分布的一个参数，常被称为率参数（rate parameter）。即每单位时间发生该事件的次数。指数分布的区间是[0,∞)。如果一个随机变量X呈指数分布，则可以写作：X ~ Exponential（λ）。随机变量X (X 的率参数是λ) 的期望值是：

\[\mathbf { E } [ X ] = \frac { 1 } { \lambda }\]

X 的方差是：

\[\mathbf { D } [ X ] = \frac { 1 } { \lambda ^ { 2 } }\]

其累积分布函数为：

\[F ( x ; \lambda ) = \left\{ \begin{aligned} 1 - e ^ { - \lambda x } & , x \geq 0 \\ 0 & , x < 0 \end{aligned} \right.\]

指数分布可以看成是泊松分布的k=0时的特例，因为“事件发生间隔T的概率等于在T单位时间内，事件发生次数为0的概率”，比方说：如果你平均每个小时接到2次电话，那么你预期等待每一次电话的时间是半个小时。

指数函数的一个重要特征是无记忆性（Memoryless Property，又称遗失记忆性）。这表示如果一个随机变量呈指数分布，它的条件概率遵循：

举例来讲就是：有一颗灯，平均5分钟闪一次，每个时刻闪的可能性是一样的，那么，假设你观察了10分钟，灯都没闪，之后等到灯闪的预期时间还是5分钟，这个5分钟的预期时间不会因为你已经等了多久而改变（无记忆性的表现）。

参数估计λ的估计：给定独立同分布样本\(x = \left( x _ { 1 } , \dots , x _ { n } \right)\)，λ的似然函数（Likelihood function）是：

其中：\(\overline { x } = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } x _ { i }\)是样本均值。似然函数对数的导数是：

率参数的最大似然（Maximum likelihood）估计值是：\(\widehat { \lambda } = \frac { 1 } { \overline { x } }\)。记住末尾的结论即可。

指数分布的应用

一个设备出现多次故障的时间间隔记录如下：

23, 261, 87, 7, 120, 14, 62, 47, 225, 71, 246, 21, 42, 20, 5, 12, 120, 11, 3, 14, 71, 11, 14, 11, 16, 90, 1, 16, 52, 95

根据上面数据，我们可以计算得到该设备发生故障的平均时间是59.6小时，即单位小时时间内发生故障事件的次数λ=1/59.6=0.0168。 那么该设备在3天（72小时)内出现故障的概率是多大呢？即求P(x<72)，这就需要计算指数分布的累积分布函数：

也即该设备3天内出现故障的概率大于70%。

正态分布

正态分布（英语：normal distribution）又名高斯分布（英语：Gaussian distribution），是一个非常常见的连续概率分布。其优美性在于很多自然界中的概率分布、误差分布都满足于正态分布³。

若随机变量\(X\)服从一个位置参数为\(\mu\) 、尺度参数为\(\sigma\)的正态分布，记为：

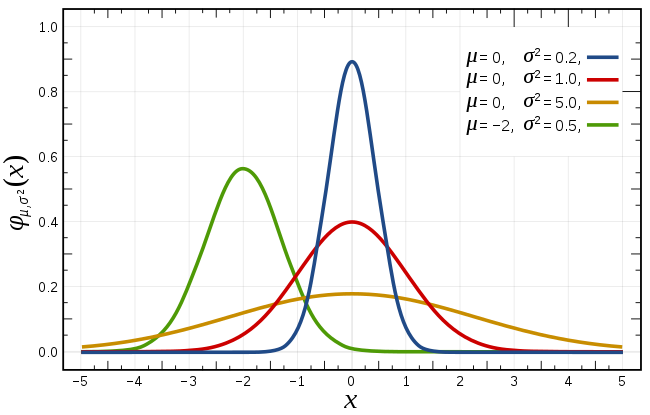
\[X \sim N \left( \mu , \sigma ^ { 2 } \right)\]

则其概率密度函数为:

\[f ( x ) = \frac { 1 } { \sigma \sqrt { 2 \pi } } e ^ { - \frac { ( x - \mu ) ^ { 2 } } { 2 \sigma ^ { 2 } } }\]

图像为:

正态分布的数学期望值或期望值\(\mu\)等于位置参数，决定了分布的位置；其方差\(\sigma^2\)的开平方或标准差\(\sigma\)等于尺度参数，决定了分布的幅度。

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线（类似于寺庙里的大钟，因此得名）。我们通常所说的标准正态分布是位置参数\(\mu =0\)，尺度参数\(\sigma^2 = 1\)的正态分布（见图中红色曲线）。

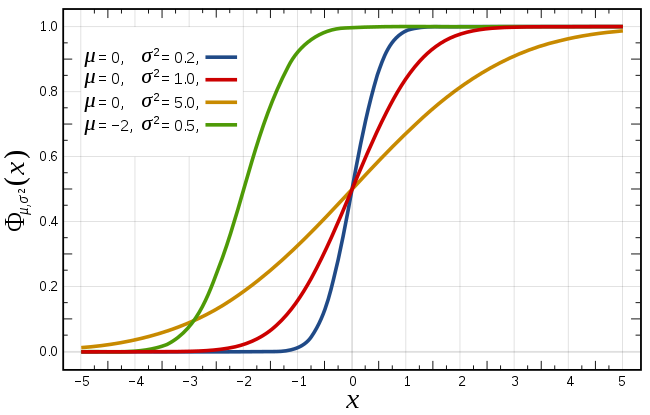
其累积分布函数是指随机变量\(X\)小于或等于\(x\)的概率，用概率密度函数表示为：

\[F ( x ; \mu , \sigma ) = \frac { 1 } { \sigma \sqrt { 2 \pi } } \int _ { - \infty } ^ { x } \exp \left( - \frac { ( t - \mu ) ^ { 2 } } { 2 \sigma ^ { 2 } } \right) d t\]

正态分布有一个非常重要的性质：在特定条件下，大量统计独立的随机变量的平均值的分布趋于正态分布，这就是中心极限定理。中心极限定理的重要意义在于，根据这一定理的结论，其他概率分布可以用正态分布作为近似。

参数为\(n\)和\(p\)的二项分布，在\(n\)相当大而且\(p\)接近0.5时近似于正态分布（有的参考书建议仅在\(n p\)与\(n(1−p)\)至少为5时才能使用这一近似）。近似正态分布平均数为\(\mu = n p\)且方差为\(\sigma^2 = n p (1 - p)\).

泊松分布带有参数λ当取样样本数很大时将近似正态分布λ。近似正态分布平均数为\(\mu = \lambda\)且方差为\(\sigma^2 = \lambda\)。

当我们已知一个事件的概率满足正态分布时，我们可以采用采样的方法估算其正态分布参数：计算采样结果的平均值即为其数学期望\(\mu\)，采样结果的方差为\(\sigma^2\)。

正态分布的应用

对于社会上遇到的大部分问题，其概率分布规律基本都满足正态分布，为了计算某种概率，我们就可以通过数学建模利用正态分布方便解决问题。

一般来说，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布（见中心极限定理）。从理论上看，正态分布具有很多良好的性质 ，许多概率分布可以用它来近似；还有一些常用的概率分布是由它直接导出的，例如对数正态分布、t分布、F分布等。

杰恩斯(E.T.Jaynes)在《Probability Theory: the Logic of Science》提出了两个问题：

1. 为什么正态分布被如此广泛的使用？
2. 为什么正态分布在实践使用中非常的成功？

Jaynes指出，正态分布在实践中被广泛地成功应用，主要是因为正态分布具有在数学上的多种稳定性质，这些性质包括：

• 两个正态分布密度的乘积还是正态分布
• 两个正态分布密度的卷积还是正态分布，也就是两个正态分布的和还是正态分布
• 正态分布\(N ( \mu , \sigma ^ { 2 })\)的傅立叶变换还是正态分布
• 中心极限定理保证了多个随机变量的求和效应将导致正态分布
• 正态分布和其它具有相同方差的概率分布相比，具有最大熵

前三个性质说明了正态分布一旦形成,就容易保持该形态的稳定，Landon对于正态分布的推导也表明了，正态分布可以吞噬较小的干扰而继续保持形态稳定。后两个性质则说明，其它的概率分布在各种的操作之下容易越来越靠近正态分布。正态分布具有最大熵的性质，所以任何一个对指定概率分布的操作，如果该操作保持方差的大小，却减少已知的知识，则该操作不可避免地增加概率分布的信息熵，这将导致概率分布向正态分布靠近。

正由于正态分布的稳定性质，使得它像一个黑洞一样处于一个中心的位置，其它的概率分布形式在各种操作之下都逐渐向正态分布靠拢，Jaynes把它描述为概率分布中重力现象(gravitating phenomenon)。

我们在实践中为何总是选择使用正态分布呢，正态分布在自然界中的频繁出现只是原因之一。Jaynes认为还有一个重要的原因是正态分布的最大熵性质。在很多时候我们并不知道数据的真实分布是什么，但是一个分布的均值和方差往往是相对稳定的。因此我们能从数据中获取到的比较好的知识就是均值和方差，除此之外没有其它更加有用的信息量。因此按照最大熵原理，我们应该选择在给定的知识的限制下，选择熵最大的概率分布，而这就恰好是正态分布。因此按照最大熵的原理，即便数据的真实分布不是正态分布，由于我们对真实分布一无所知，如果数据不能有效提供除了均值和方差之外的更多的知识，那这时候正态分布就是最佳的选择。

不同概率分布之间的关系

不同概率分布之间的关系前面描述有所表述。

在二项分布的伯努利试验中，如果试验次数n很大，二项分布的概率p很小，λ比较稳定，且乘积λ = np比较适中（λ比较小导致np增长速度较慢或者存在有限值，经验法则是n≥20，p≤0.05）²，则事件出现的次数的概率可以用泊松分布来逼近。事实上，二项分布可以看作泊松分布在离散时间上的对应物。反之，如果 np 趋于无限大（如 p 是一个定值），则根据德莫佛-拉普拉斯(De’Moivre-Laplace)中心极限定理，这列二项分布将趋近于正态分布。

二项分布的极限是泊松分布，泊松分布的极限是正态分布，由于二项分布和泊松分布都是离散型数据，所以只有当n或者λ很大的时候，可近似认为其X轴为连续，才能用正态分布来模拟。当λ≥20时，泊松分布可以用正态分布来近似，当λ≥50，泊松分布基本上就等于正态分布了。由此可见，当离散数据的值足够大时，可以当成连续数据来分析。

在《二项分布、泊松分布到底该如何近似计算》⁴中，用软件计算了不同\(n\)、\(p\)下二项分布和泊松分布之间的数据差异，并验证下面这个经验值：

二项分布当\(np\)和\(n(1-p)\)均大于或等于5时，泊松分布当λ≥20时，用正态分布可以很好地近似计算

参考