介绍
Cuckoo 哈希1是一种查找开销十分稳定(constant time worst-case complexity for lookups)的哈希算法，这是其相较于开放地址法、链表法的显著特征。
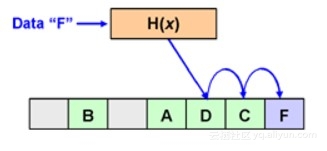
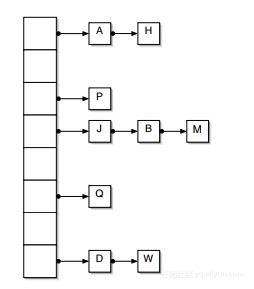
Cuckoo 哈希可以视作是开放地址法的一种进阶，其基础算法描述为：在一个由一维数组构成的哈希表\(T\)中，采用两个哈希函数(\(h_1,h_2\))，使得任意一个元素在哈希表中存在 2 个存储位置：
- 当查询哈希表中元素\(x\)时，我们分别通过两个哈希函数(\(h_1,h_2\))计算出其 2 个可能存在的位置，然后进行(并行)查询，如果在\(T[h_1(x)]\)或\(T[h_2(x)]\)位置存在元素\(x\)，则存在。否则，不存在。
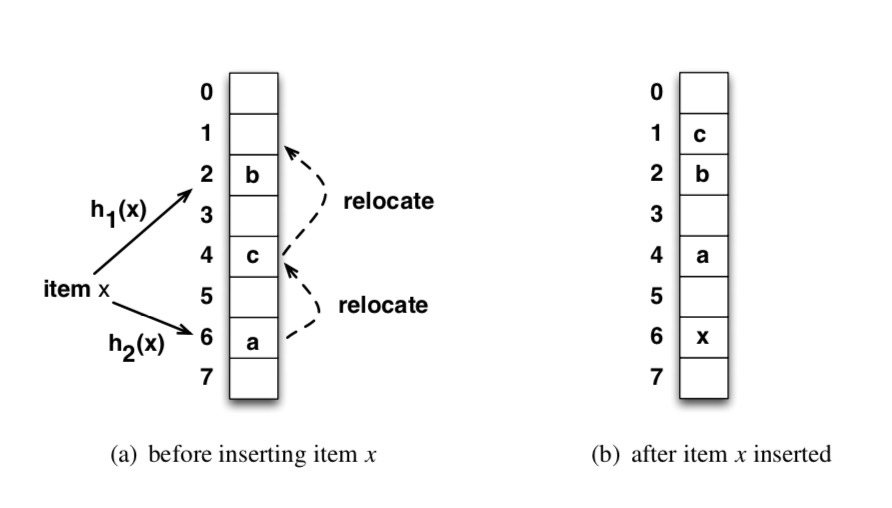
- 当在哈希表中插入元素\(x\)时，我们先进行查询，如果\(x\)已经存在，直接返回。否则，我们按照 2 个哈希函数顺序，依次计算其位置\(i = h_1(x), j = h_2(x)\)，如果\(T[i]/T[j]\)任一位置空闲，则将\(x\)放置在其中一个位置上；如果 2 个位置都不空闲，则可以将\(T[i]\)位置的元素\(y\)拿出，然后将\(x\)放置在\(T[i]\)的位置上，然后将\(y\)放置在\(h_1(y),h_2(y)\)中的另一个位置上去，以此递归，如果\(y\)所属的另一个位置仍被占用，则再将其拿出，再次放置，细节如下图所示；当递归踢元素的此处到达一定次数，则我们可以判定当前哈希表已经满了，需要重构哈希表大小。
- 当在哈希表中删除元素\(x\)时，按照查询的逻辑找到\(x\)所属位置，将其直接删除即可。
- 在一维空间上，Cuckoo 哈希的填充率上限差不多时 50%，要提高填充率需要增加哈希表关联的维度，后面会提到。
变种
2-array 实现
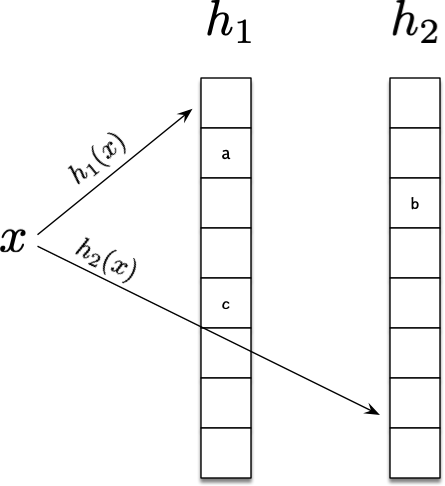
如图所示，是一种比较常见的变种实现，其采用两个数组分别关联一个哈希函数，然后放置元素、踢出元素在这两个数组之间进行，元素\(x\)在第一个数组中的位置是\(h_1(x)\)，在第二个数组中的位置是\(h_2(x)\)。该种实现有在线可视化的操作动画2。
D-Cuckoo Hashing
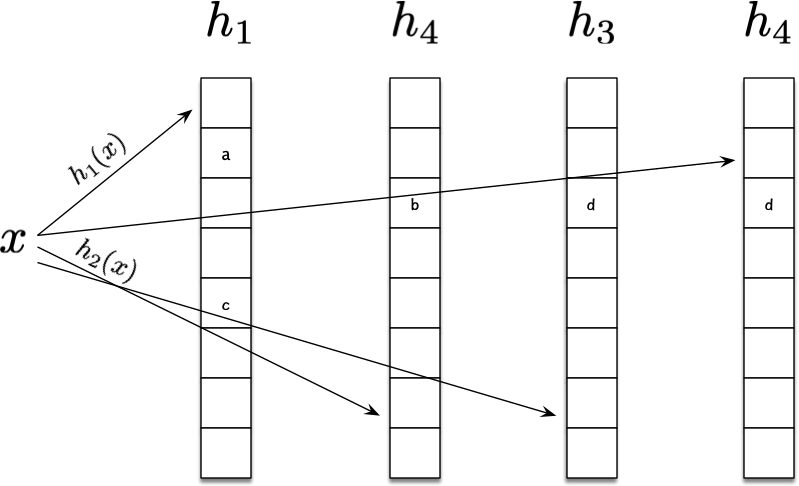
将常见的 2 数组实现扩展到多层实现，同时搭配多种哈希函数，如下图扩展到 4 层数组，这样能一定程度提高整体的填充率，减少rehash的次数。RocksDB实现了基于多层Cuckoo Hashing的 SST 文件结构3，最多支持 64 层 hash 表。充分利用其高效的查找优势。当Cuckoo Hash表层数增多时，哈希冲突时，找到适合踢出的元素就是一件复杂的事情了，RocksDB采用广度优先搜索来搜索最合适踢出的元素。
Cuckoo Filter
cuckoo filter4是基于Cuckoo Hashing延伸出来的判断存在性的数据结构，功能性上与bloom filter一样。为了提高空间填充率，其也增加了 hash 数组空间，但是采用了和RocksDB不同的策略：
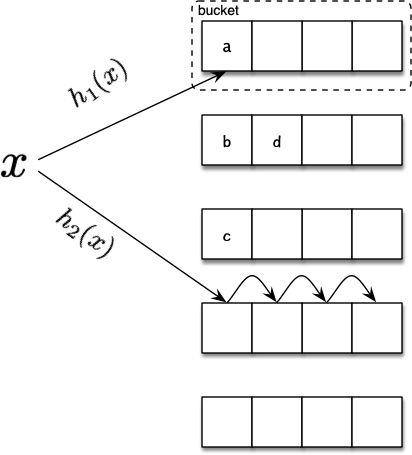
其中采用单层bucket数组的原始方案，但是每个bucket能够容纳的元素扩展为b个(如图b=4)，这样使得元素被踢出后，可以用快速、简单的方法找到其另一个bucket位置。由于只判断存在性，允许假阳性，为了节省空间，bucket中每个entry只存储对应元素的fingerprint(一种普通哈希值即可，通常为 1byte 信息)，然后定位所属bucket位置时，在根据如下两种哈希公式计算(一共三种 hash 值)：
\[\begin{aligned} & i = h_1(x) = hash(x) \\ & j = h_2(x) = h_1(x) \oplus hash(x's fingerprint) \\ \end{aligned}\]这样设计的必要性是，由于cuckoo filter中存储的是元素的fingerprint，已经丢失了大量信息，当该元素被踢出时，无法再次通过 hash 计算其对应对应的另一个bucket的位置，因此其中利用了异或(\(\oplus\))的特性，i、j可以分别又对方异或(\(\oplus\))上\(hash(fingerprint)\)计算得出：
\[\begin{aligned} & i = j \oplus hash(fingerprint) \\ & j = i \oplus hash(fingerprint) \\ \end{aligned}\]其增删改查方法也比较基本：
一些需要注意的点：
- 假如出现了三个 hash 值完全相等的两个元素(\(fingerprint/h_1/h_2\))，仍然按照算法正常运行，后果仅仅是对应的bucket中的entry存在两个相同的元素(fingerprint)而已，并不影响该数据结构的增删改查；删除其中之一时，删除其中一个元素(fingerprint)即可；当每个bucket有b个entry时，可以支持最多2b个三个 hash 值完全相等的元素，可以由相关计算，如果选用比较均匀的 hash 函数，一个数据集中数据能够重复到达2b的概率是十分的低的；
- 不建议元素重复添加，添加元素前先采用其他结构去重根据这套算法，否则，人为增加了三个 hash 值完全相等的概率；
- 由于哈希碰撞存在的可能性，不支持删除不在集合中的元素。
但是其相比bloom filter优势在于：
- CPU cache line 亲和性更高，更能够利用 CPU 硬件特性进行加速。可以通过一维数组实现多entry的bucket数组，由于 CPU cache line 的特性，使得查询bucket的每个entry速度更快，而bloom filter要访问分布在多个位置的 bit 信息，完全不能利用 CPU cache line。
- 查询时间复杂度更低，永远只查询固个数的数据；
- 占用存储空间更低，填充率高，如下图，当每个bucket有 4 个entry时，每个最总填充率能到达 95%，而且每个entry大于 8bit 后，填充率提升不大，因此每个entry只需要存储 8bit 的fingerprint数据，总和计算下来，cuckoo filter每个元素只需要占用 12bit 空间，而bloom filter需要用到 13bit；
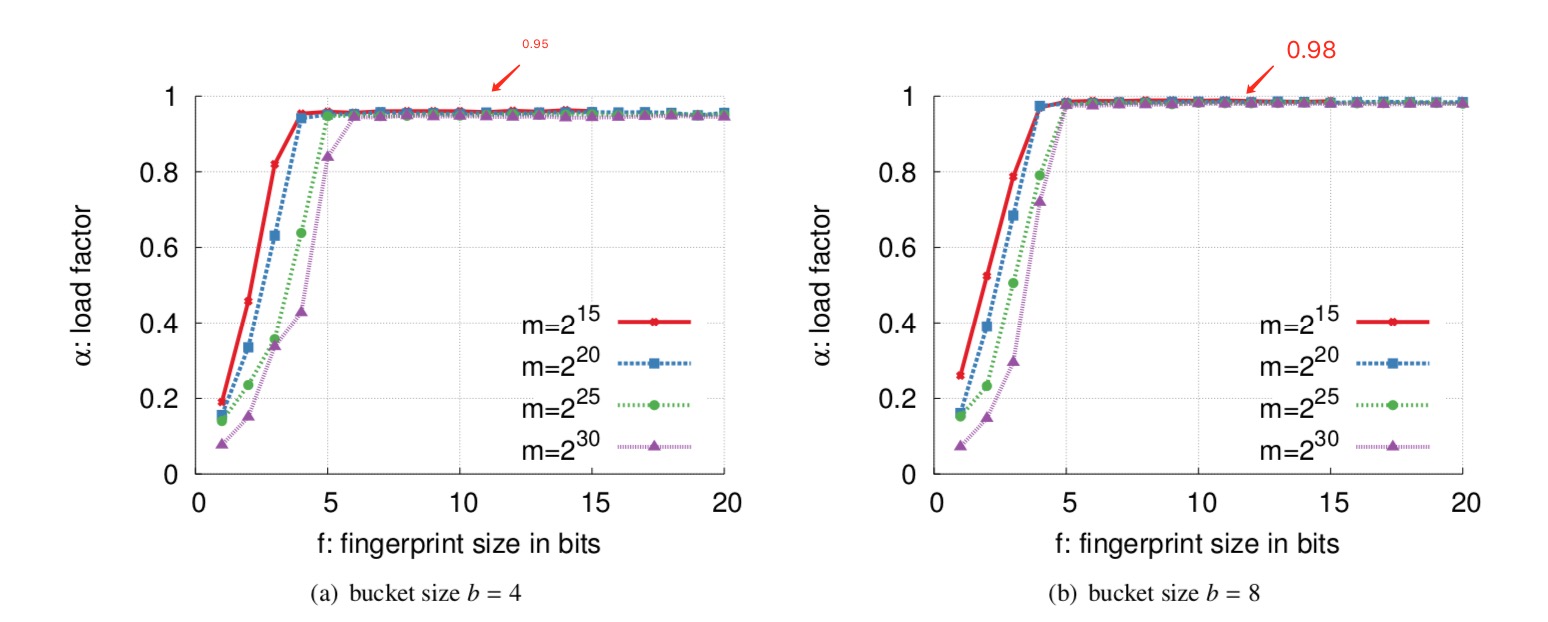
- 假阳性概率更低，从上图可以看出；
- 支持删除元素。
其一个开源实现libcuckoo。
局限性/适用场景
Cuckoo Hash在填充率过高时，添加元素变得困难，通常适用于一些读多写少的场景。而且Cuckoo Hash的读写操作都需要访问 2 个以上的bucket，使得读写方法的难以并发执行，而且rehash也难以开销分摊，无论是无锁算法、或者减小锁粒度都是很困难的一件事：
- 死锁风险，Cuckoo Hash的读写操作都需要访问 2 个以上的bucket，而且两个bucket的上锁顺序也按照特定顺序，这就大大增加了多个元素并发访问时，死锁的风险；
- 假丢失数据，当某个元素被踢出并且还未插入另一个对应位置时，如果同时有查询该元素的请求到达时，可能会误判数据丢失。
MemC35实现了concurrent cuckoo hashing，通过很多努力，实现了多读单写并发的(multiple-reader/single writer concurrent access)的cuckoo hashing：
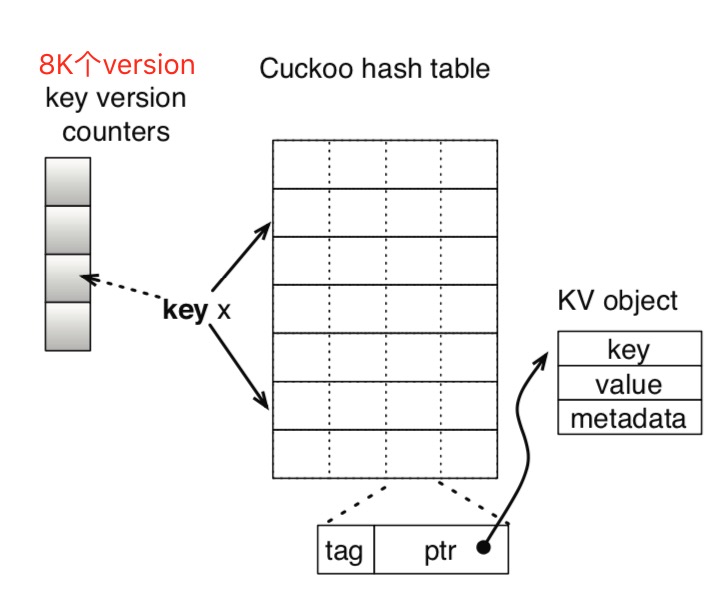
- 其基础结构与前面cuckoo filter的设计类似，每个bucket可以存储四个元素，使得填充率到达 90% 以上；
- 为了充分发挥 CPU cache line 的特性，在每个 entry 上增加了一个 1byte 的 tag，减少指针解引用的次数，平均每次调用
lookup方法时，只有 0.03 次指针解引用(97% 的概率被 tag 比较拦截)； - 采用原子操作变更数据，放弃了排他锁。为了避免在读写并发时读到不新鲜的数据，采用数据版本检测的方法。写方法一开始会更新对应元素的版本，读方法开始和结束时，会分别读取一次版本，如果版本一直，则表示，读取过程中数据没有发生并发修改，否则，发生了改变，重新读取一次。这样就使得每个元素都需要一个内存存储版本，为了提高内存填充率，这里预分配了 8K 个
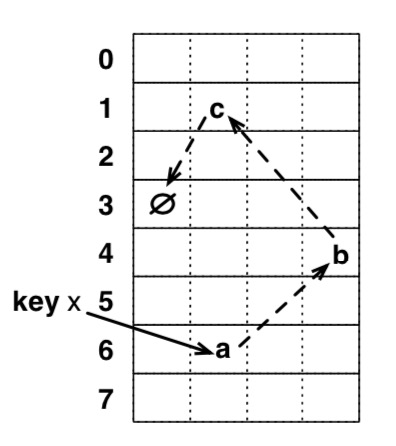
版本计数器，将全部元素经过 hash 分配到不同版本计数器上，即每个版本计数器负责管理一批 hash 相同的元素。经过检验，在正常使用中只有0.01%的概率会触发读取重试的逻辑； - 为了避免假丢失数据，其会先搜索出需要踢出操作的元素顺序，然后按照顺序反向踢出。如下图，其搜索出需要踢出的顺序(a=>b=>c)后，然后先将c的entry数据复制到另一个所属bucket后，再将b的entry数据复制到原来c的位置，这样就保证在踢出过程中，没有数据会出现丢失假象。
