基本概念
中心极限定理
在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。通俗来讲就是多次采样的样本均值满足正态分布,亦或:
中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取 n 个抽样,一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。1
零假设
在推论统计学中,零假设(英语:null hypothesis,又译虚无假设、原假设,符号:\(\boldsymbol { H } _ { 0 }\))是做统计检验时的一类假设。零假设的内容一般是希望能证明为错误的假设,或者是需要着重考虑的假设。在相关性检验中,一般会取“两者之间无关联”作为零假设,而在独立性检验中,一般会取“两者之间非独立”作为零假设。
备择假设
与零假设相对的是备择假设(或对立假设),即希望证明是正确的另一种可能。从数学上来看,零假设和备择假设的地位是相等的,但是在统计学的实际运用中,常常需要强调一类假设为应当或期望实现的假设。如果一个统计检验的结果拒绝零假设(结论不支持零假设),而实际上真实的情况属于零假设,那么称这个检验犯了第一类错误。反之,如果检验结果支持零假设,而实际上真实的情况属于备择假设,那么称这个检验犯了第二类错误。通常的做法是,在保持第一类错误出现的机会在某个特定水平上的时候(即显著性差异值或α值),尽量减少第二类错误出现的概率。
第一型及第二型错误
第一型及第二型错误(英语:Type I error & Type II error)或型一错误及型二错误为统计学中推论统计学的名词。
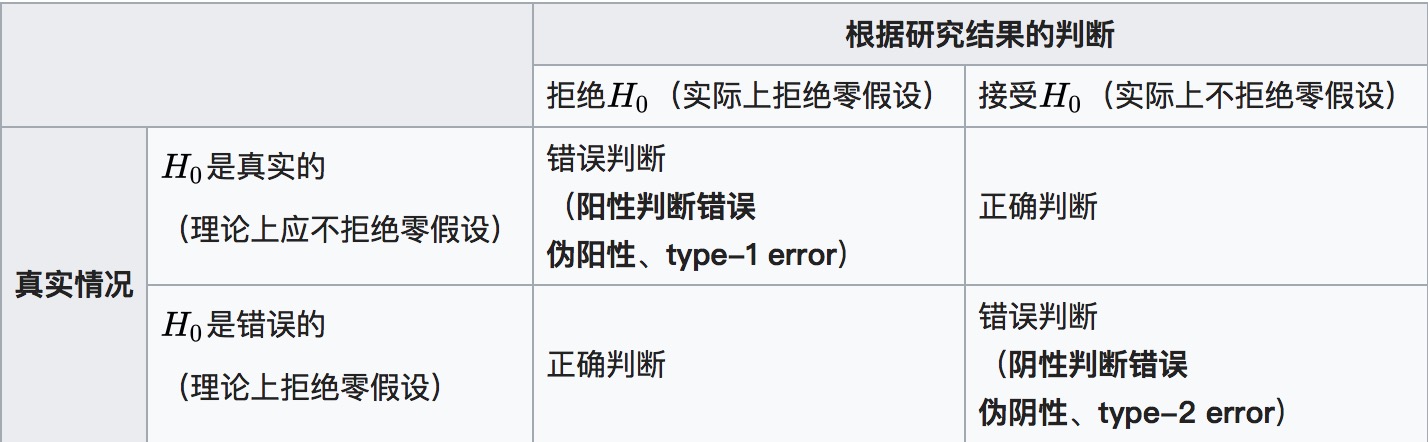
在假设检验中,有一种假设称为“零假设(虚无假设)”。假设检验的目的就是利用统计的方式,推测零假设是否成立。若零假设(虚无假设)事实上成立,但统计检验的结果不支持零假设(拒绝零假设),这种错误称为第一型错误。若零假设事实上不成立,但统计检验的结果支持零假设(接受零假设),这种错误称为第二型错误。
假设检验
假设检验是推论统计中用于检验统计假设的一种方法。而“统计假设”是可通过观察一组随机变量的模型进行检验的科学假说。一旦能估计未知参数,就会希望根据结果对未知的真正参数值做出适当的推论。
统计上对参数的假设,就是对一个或多个参数的论述。而其中欲检验其正确性的为零假设(null hypothesis),零假设通常由研究者决定,反映研究者对未知参数的看法。相对于零假设的其他有关参数之论述是备择假设(alternative hypothesis),它通常反应了执行检定的研究者对参数可能数值的另一种(对立的)看法(换句话说,备择假设通常才是研究者最想知道的)。
基本原理
假设检验的分析方法包含两条基本的原理:带概率性质的反证法原理和小概率事件原理2。
带概率性质的反证法原理
反证法(Proof by Contradiction),又称为归谬法、背理法。在证明数学问题时,先假定命题结论的反面成立,在这个前提下,若推出的结果与定义、公理、定理相矛盾,或与命题中的已知条件相矛盾,或与假定相矛盾,从而证明命题结论的反面不可能成立,由此断定命题的结论成立。
反证法证明命题的一般步骤如下:
- 假设结论的反面成立,即反设;
- 由这个假设出发,经过正确的推理导出矛盾,即归谬;
- 由矛盾判定假设不正确,从而肯定命题结论正确,即结论。
这三个步骤中,归谬是最重要的,常见的归谬包括这三类:与已知条件矛盾;与已知的公理、定理、定义矛盾;自相矛盾。
在数学中,\(\sqrt{2}\) 是无理数就是用反证法证明的。证明过程如下:
- 第一步,反设:如果\(\sqrt{2}\)是有理数,则必有:\(\sqrt { 2 } = \frac { p } { q }\),其中p,q是互质的正整数。
- 第二步,归谬:两边平方,则有: \(\begin{aligned} 2 & = \frac { p ^ { 2 } } { q ^ { 2 } } \\ p ^ { 2 } & = 2 q ^ { 2 } \end{aligned}\) 则\(p\)为偶数,设\(p=2r\),则有: \(\begin{array} { c } { 4 r ^ { 2 } = 2 q ^ { 2 } } \\ { 2 r ^ { 2 } = q ^ { 2 } } \end{array}\) 则\(q\)也是偶数,这与p、q互质矛盾。
- 第三步,结论:因此假设不成立,\(\sqrt{2}\)是无理数。
假设检验所使用的反证法与此最大的不同点是带有概率,即用概率来判断命题是否成立。费歇尔老先生在提出显著性水平检验时,先假设总体的参数,这就是原假设(Null Hypothesis),如小麦的植株高度往年统计的均值为90cm。今年要对种植结果进行验证,在验证之前假设总体均值仍然是90cm,然后抽样检验。如果今年的小麦植株高度还是90cm,那么样本的均值应该与90cm差不多,如果差得很远,比如105cm,或者只有70cm,抽样结果就显得很不合理,因此就可以推翻原假设,即今年的小麦植株高度不是90cm。但是这种判断是存在出错可能的,因为即使今年的植株高度还是90cm,但植株高度是服从某种分布的,有可能会抽出大于105cm或小于70cm的样本的,虽然这个概率很小。因此在费老先生所提出的显著性水平检验中,所运用的反证法是带有概率的,也就是说对于抽样结果的判断是有出错的可能性的。
注意费歇尔并没有告诉你拒绝原假设后你应该接受什么,而奈曼-皮尔逊则在此基础上给出了第二个假设,即备择假设(Alternative Hypothesis)。这个假设是与原假设相对立的,在拒绝原假设的同时可以接受备择假设。
小概率事件原理
如何判断抽样结果是不是不合理呢?费歇尔老先生提出了p-value这个概念,用来表示在原假设成立的条件下,抽样结果的不合理和更不合理的概率。他还给出了一个判决点,即0.05,费歇尔p值小于1/20就足以拒绝原假设了。
0.05是足够小的概率3,一般认为,在一次抽样(试验)中,小概率事件几乎不可能发生,如果出现发生了,则说明事先的假设是错误的。但小概率事件并不是一定不会发生,当抽样次数足够多时,小概率事件是一定会发生的。这说明即使是一次抽样,小概率事件仍有可能发生,也就是说存在判断错误的可能性。
显著性水平
这里0.05被称为显著性水平,用α表示。其值的意义,可以被解释为:发生第一型错误的概率
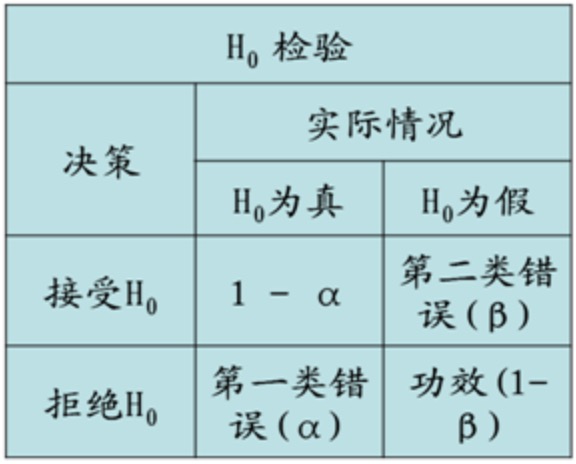
那么,100% * (1-α)则是置信水平,关于置信水平和拒绝域的选择判定,可以参考《假设检验》4。
假设检验步骤
假设检验大致有如下步骤:
- 最初研究假设为真相不明。
- 第一步是提出相关的零假设和备择假设。这是很重要的,因为错误陈述假设会导致后面的过程变得混乱。
- 第二步是考虑检验中对样本做出的统计假设;例如,关于独立性的假设或关于观测数据的分布的形式的假设。这个步骤也同样重要,因为无效的假设将意味着试验的结果是无效的。
- 决定哪个检测是合适的,并确定相关检验统计量 T。
- 在零假设下推导检验统计量的分布。在标准情况下应该会得出一个熟知的结果。比如检验统计量可能会符合t-分布或正态分布。
- 选择一个显著性水平 (α),若低于这个概率阈值,就会拒绝零假设。最常用的是 5% 和 1%。
- 根据在零假设成立时的检验统计量T分布,找到数值最接近备择假设,且机率为显著性水平 (α)的区域,此区域称为“拒绝域”,意思是在零假设成立的前提下,落在拒绝域的机率只有α。
- 针对检验统计量T,根据样本计算其估计值tobs。
- 若估计值tobs未落在“拒绝域”,接受零假设。若估计值tobs落在“拒绝域”,拒绝零假设,接受备择假设。
举例阐述可以参考《假设检验之三:假设检验的基本步骤》
比较分析
在假设检验的过程中有很重要的一步,就是选取假说的比较分析。所谓比较分析5,就是运用假设检验原理,通过抽样,对总体的某些参数(常用均值或方差)的大小进行比较,得出因子的不同状态对结果是否产生显著影响。比较对象可以是连续数据,也可以是离散数据。这种比较只给出“是”与“否”的结论,不试图给出具体的差异值。
比较分析有哪些种?
比较分析内容庞大,有不同的分类方法。首先是参数检验和非参数检验。
所谓参数检验,就是基于确认的总体分布,针对分布的参数,如均值、标准差、比率等所做的抽样检验。有的解释说总体服从正态分布,这种说法不够全面。对于连续数据来说,如果能够确认总体服从某个分布,也可以通过变换使其服从正态分布,从而可以运用抽样分布来做出推断;对于离散数据来说,也有基于二项分布和泊松分布的检验。
非参数检验,则是针对总体不服从正态分布,即使通过变换也不能满足正态分布的要求的情况下所采用的检验方法。它不对分布的参数来进行推断,因此在判断的精确性上要比参数检验弱一些。当然有个别方法可以媲美参数检验,比如大家熟知的Wilcoxon检验。
针对参数检验,又可以根据数据的性质分为两大类,即连续数据和离散数据两类。
连续数据的参数检验又可以根据分组的数量分为两大类。组数为1和2时,采用的是经典的检验,即\(Z\)、\(t\)、\(\chi ^{2}\)和\(F\)检验;当组数≥3时,则需要用到方差分析(ANOVA)。
离散数据的参数检验类似,组数为1和2时,采用二项分布或泊松分布来做检验,当然在满足正态近似条件时可以用正态分布来分析;当组数≥3时,则需要用到列联表来分析了。
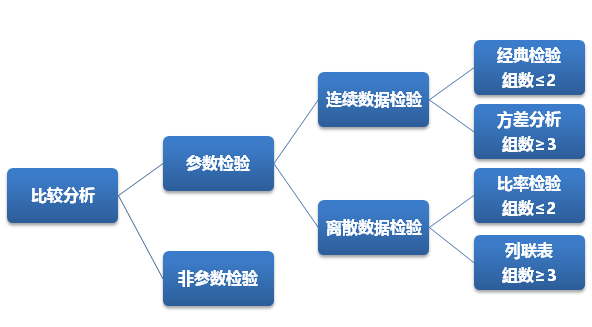
比较分成五类,就是经典比较、方差分析、比率检验、列联表、非参数,这五类比较采用的方法存在显著的差异:
- 经典比较:包括大家非常熟悉的\(Z\)-检验、\(t\)-检验、\(\chi ^{2}\)检验、\(F\)-检验。
- 方差分析:包含的内容实在是太广泛了,而针对比较分析来说,一般是指单因子和两因子方差分析。
- 比率检验:主要是单样本或两样本服从二项分布和泊松分布的比率检验。
- 列联表:常用的就是大家熟知的R*C表了,当然还有很复杂的应用。
- 非参数检验:统计学家们为不服从特定分布的数据研发了很多检验方法。
下面先讲讲经典比较中常见的几种参数检验,在经典比较通常都需要计算对应检验的p值(p-value),因此我们先需要了解p值的意义,这里可以参考《假设检验之八:p值是什么》6。简单可以理解为p值代表了样本偏离总体中心的程度,多数分布曲线(t分布、Z分布)都是近似对称为钟型曲线,当样本处于曲线的两个末端时,代表其偏离程度过大,p值以面积来代表这种偏离程度。
T检验
学生t检验(英语:Student’s t-test)常作为检验一群来自正态分配总体的独立样本之期望值的是否为某一实数,或是二群来自正态分配总体的独立样本之期望值的差是否为某一实数。举个简单的例子,也就是说我们可以在抓取一个班级的男生,去比较该班与全校男生之身高差异程度是不是推测的那样,或是不同年级班上的男生身高的差异的场合是否一如预期使用此检验法。今日,它更常被应用于小样本判断的置信度。
最常用t检验的情况有:
- 单样本检验:检验一个正态分布的总体的均值是否在满足零假设的值之内(样本均数与已知总体均数的比较),例如检验一群军校男生的身高的平均是否符合全国标准的170公分界线。
适用条件:
- 样本来自于正态分布的群体(当样本量足够大,即使原数据不服从正态分布,由中心极限定理可知,其样本均数的抽样分布仍然是正态的。因此当样本量较大时,研究者很少去考虑单样本t检验的适用条件,此时真正会限制该方法使用的是均数是否能够代表相应数据的集中趋势,只要数据分布不是强烈的偏态,一般而言单样本t检验都是适用的。)
- 样本量较小(通常 n < 30,n较小时,一般要求样本取自正态总体)
- 总体标准差未知的情况
检验零假说为一群来自正态分配独立样本\(x_i\)之总体期望值\(\mu\)为\(\mu_0\)可利用以下统计量
\[t = \frac { \overline { x } - \mu _ { 0 } } { s / \sqrt { n } }\]其中\(i = 1 \dots n\),\(\overline { x } = \frac { \sum _ { i = 1 } ^ { n } x _ { i } } { n }\)为样本平均数,\(s = \sqrt { \frac { \sum _ { i = 1 } ^ { n } \left( x _ { i } - \overline { x } \right) ^ { 2 } } { n - 1 } }\)为样本标准偏差,\(n\)为样本数。该统计量\(t\)在零假说:\(\mu = \mu _ { 0 }\)为真的条件下服从自由度为\(n − 1\)的\(t\)分布。
大量检测已知正常人血浆载脂蛋白E( apo E)总体平均水平为4.15mmol/L。某医师经抽样测得41例陈旧性心机梗死患者的血浆载脂蛋白E平均浓度为5.22mmol/L,标准差为1.61mmol/L。据此能否认为陈旧性心肌梗死患者的血浆载脂蛋白E平均浓度与正常人的平均浓度不一致?
- 建立假设、确定检验水准α=0.05,双侧检验,自由度为
40-1 = 40H0:μ = μ0 (零假设null hypothesis,即与正常人浓度一致) H1:μ ≠ μ0(备择假设alternative hypothesis,即与正常人浓度不一致) - 计算检验统计量,根据上面的公式计算得\(t = \frac { \overline { x } - \mu _ { 0 } } { s _ { \overline { x } } } = \frac { \overline { x } - \mu _ { 0 } } { s / \sqrt { n } } = \frac { 5.22 - 4.15 } { 1.61 / \sqrt { 41 } } = 4.26\)
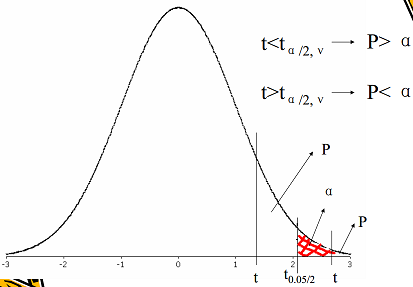
- 确定p值和作出推断结论。查t分布表7, t0.05/2,40=2.021, t=4.26>t0.05/2,40,p < 0.05(如下图,t分布在t>0侧为减函数)。按α=0.05水准,拒绝H0,接受H1,可认为陈旧性心肌梗死患者的血浆载脂蛋白E平均浓度与正常人的差别有统计学意义,结合专业可以认为前者平均浓度较高。
- 双样本检验:其零假设为两个正态分布的总体的均值之差为某实数,例如检验二群人的身高之平均是否相等。这一检验通常被称为学生t检验。但更为严格地说,只有两个总体的方差是相等的情况下(
方差齐性)8,才称为学生t检验;否则,有时被称为Welch检验。以上谈到的检验一般被称作“未配对”或“独立样本”t检验,我们特别是在两个被检验的样本没有重叠部分时用到这种检验方式。具体内容参考维基百科#独立双样本t检验。
- “配对”或者“重复测量”t检验:
检验同一统计量的两次测量值之间的差异是否为零。举例来说,我们测量一位病人接受治疗前和治疗后的肿瘤尺寸大小。如果治疗是有效的,我们可以推定多数病人接受治疗后,肿瘤尺寸应该是变小了。
配对样本t检验可视为单样本t检验的扩展,不过检验的对象由一群来自正态分配独立样本更改为二群配对样本之观测值之差。若二群配对样本\(x_{1i}\)与\(x_{2i}\)之差为\(d_i = x_{1i} − x_{2i}\)独立且来自正态分配,则\(d_i\)之总体期望值μ是否为\(\mu_0\)可利用以下统计量:
\[t = \frac { \overline { d } - \mu _ { 0 } } { s _ { d } / \sqrt { n } }\]其中\(i = 1 \ldots n\),\(\overline { d } = \frac { \sum _ { i = 1 } ^ { n } d _ { i } } { n }\),为配对样本差值之平均数,\(s _ { d } = \sqrt { \frac { \sum _ { i = 1 } ^ { n } \left( d _ { i } - \overline { d } \right) ^ { 2 } } { n - 1 } }\),为配对样本差值之标准偏差,n为配对样本数。该统计量t在零假说:\(\mu = \mu_0\)为真的条件下服从自由度为\(n − 1\)的t分布。
例如:将大白鼠配成8对,每对分别饲以正常饲料和缺乏维生素E饲料,测得两组大白鼠肝中维生素A的含量,试比较两组大白鼠中维生素A的含量有无差别。
大白鼠配对号 正常饲料组 维生素E缺乏组 差数d 1 3550 2450 1100 2 2000 2400 -400 3 3000 1800 1200 4 3950 3200 750 5 3800 3250 550 6 3750 2700 1050 7 3450 2500 950 8 3050 1750 1300 Mean 3318.75 2506.25 812.5 解题:建立检验假设和确定检验水准。H0: μd=0,H1: μd≠0,α=0.05,双侧检验;
选定检验方法和计算统计量: \(\begin{array} { l } { \overline { d } = \frac { \sum d } { n } = \frac { 1100 + -400 + \ldots + 1300} { 8 } = \frac { 6500 } { 8 } = 812.5 } \\ \frac { S _ { d } } { \sqrt { n } } = \sqrt { \frac { (1100 - 812.5) ^ { 2 } + \ldots + ( 1300 - 812.5) ^ { 2 } } {8 \times ( 8 - 1 )} } = \sqrt { \frac { 2088750 } { 56 } } = 193.1298 \\ { t = \frac { \overline { d } - \mu _ { d } } { S _ { d } / \sqrt { n } } = \frac { 812.5 - 0 } { 193.1298 } = 4.2070 , \quad v = 8 - 1 = 7 } \end{array}\)
确定P值和作出推断结论:查t分布表7(双侧), t = 4.2 > t0.05/2,7 = 2.365,P < 0.05。按 α = 0.05水准,拒绝H0,接受H1,可以认为两种饲料喂养的两组大白鼠中维生素A的含量有差别。正常饲料组比缺乏维生素E饲料组的含量要高。
- 检验一条回归线的斜率是否显著不为零。
具体内容参考维基百科#简单线性回归之斜率。
单侧检验与双侧检验:
- 在进行t检验时,如果其目的在于检验两个总体均数是否相等,即为双侧检验(因为均值的偏离为两个方向)。 例如检验某种新降压药与常用降压药效力是否相同?就是说,新药效力可能比旧药好,也可能比旧药差,或者力相同,都有可能。
- 如果我们已知新药效力不可能低于旧药效力,例如磺胺药+磺胺增效剂从理论上推知其效果不可能低于单用磺胺药,这时,无效假设为H0:μ1=μ2, 备择假设为H1: μ1>μ2 , 统计上称为单侧检验。
Z检验
Z检验,也称“U检验”,是为了检验在零假设情况下测试数据能否可以接近正态分布的一种统计测试。根据中心极限定理,在大样本条件下许多测验可以被贴合为正态分布。在不同的显著性水平上,Z检验有着同一个临界值,因此它比临界值标准不同学生t检验更简单易用。当实际标准差未知,而样本容量较小(小于等于30)时,学生T检验更加适用。
简而言之,\(Z\)检验适用于总样本正态分布,已知标准差、均值,且样本量大于30的场景。当整体标准差已知的时候,就不需要用样本标准差去估计总体标准差了。通常来说,Z分布通常用于大样本,t分布通常用于小样本,但由于t分布具有逐渐逼近正态分布的特征,使得它也可以应用于大样本,但是Z检验比较好计算。
单样本Z检验
最简单的\(Z\)检验是单样本\(Z\)检验,它检验具有已知方差的正态分布总体的均值。例如,糖果制造商的经理想要知道某个批次的糖果盒的平均重量是否等于目标值10盎司。根据历史数据,经理知道填充机器的标准差为0.5盎司,因此他们使用该值作为单样本\(Z\)检验中的总体标准差。
其统计量为:
\[Z = \frac { \overline { X } - \mu _ { 0 } } { \frac { S } { \sqrt { n } } }\]其中,\(\overline { X }\)是检验样本的平均数、\(\mu_0\)是已知总体的平均数、\(S\)是样本的标准差、\(n\)是样本容量。
例如,随机地从一批铁钉中抽取 16 枚, 测得它们的长度 (单位: 厘米) 如下9:
2.942371 2.988662 3.106234 3.109316 3.118427 3.132254
3.140042 3.170188 2.902562 3.128003 3.146441 2.978240
3.103600 3.003394 3.044384 2.849916
已知铁钉长度服从标准差为 0.1 的正态分布, 在显著性水平 α = 0.01 下, 能否认为这批铁钉的平均长度为 3 厘米? 如显著性水平为 α = 0.05 呢?
解: 这是方差已知时关于均值 μ 的假设检验问题,
\[H _ { 0 } : \mu = 3 \leftrightarrow H _ { 1 } : \mu \neq 3\]取检验统计量为\(Z = \sqrt { n } ( \overline { X } - 3 ) / 0.1\),检验的拒绝域为\(\|Z\| > u _ { \alpha / 2 }\)。由样本算得检验统计量的值为\(z \approx 2.16\),如显著性水平为 0.01, 则临界值为\(u _ { 0.005 } \approx 2.58\),跟检验统计量的值比较发现不能拒绝零假设,即不能推翻铁钉平均长度为 3 厘米的假设。
扩展:而如果显著性水平为 0.05 时,临界值为\(u _ { 0.025 } = 1.96\),此时可以拒绝零假设,认为铁钉平均长度不等于 3 厘米。这个例子说明结论可能跟显著性水平的选择有关:显著性水平越小,零假设被保护得越好从而更不容易被拒绝。
双样本Z检验
如果检验来自两个的两组样本平均数的差异性,从而判断它们各自代表的总体的差异是否显著。其Z值计算公式为:
\[Z = \frac { \overline { X } _ { 1 } - \overline { X } _ { 2 } } { \sqrt { \frac { S _ { 1 } } { n _ { 1 } } + \frac { S _ { 2 } } { n _ { 2 } } } }\]其中,\(\overline{X_1}\),\(\overline{X_2}\)是样本1,样本2的平均数;\(S_1\),\(S_2\)是样本1,样本2的标准差; \(n_1\),\(n_2\)是样本1,样本2的容量。
例如:一个赌博游戏的成功概率接近0.5,在一个月时间内,某玩家进行了74次赌博并赢了30次;在相同时期内,该测试雇员玩了103次赌博,而赢了65次。在显著水平0.05的情况下,能判定该客户是个骗子吗?
解:在该例子中,是一个二项分布的概率,由于样本比较大,因此可以近似为正态分布来看待。我们建立假设:
\[H _ { 0 } : 该玩家与测试雇员之间没有显著差异,即该玩家没有作弊 \\ \leftrightarrow \\ H _ { 1 } : 该玩家与测试雇员之间有显著差异,即该玩家有作弊倾向\]因此将二项分布的数学期望与方差带入计算Z值的公式:
\[Z = \frac { \frac { x _ { 1 } } { n _ { 1 } } - \frac { x _ { 2 } } { n _ { s } } } { \sqrt { \hat { p } ( 1 - \hat { p } ) \left( \frac { 1 } { n _ { 1 } } + \frac { 1 } { n _ { 2 } } \right) } } = \frac { \frac { 65 } { 103 } - \frac { 30 } { 74 } } { \sqrt { 0.5 \times ( 1 - 0.5 ) \left( \frac { 1 } { 103 } + \frac { 1 } { 74 } \right) } } = 2.969695\]根据Z值表10查的(Z值表的查询方法可以参考11)Z1-0.05/2 = 1.96,根据Z分布曲线可以判断这里可以拒绝H0,可以显著判断为该客户有作弊倾向。
卡方检验
卡方检验(Chi-Squared Test或\(\chi ^{2}\) Test)是一种统计量的分布在零假设成立时近似服从卡方分布(\(\chi ^{2}\)分布)的假设检验。在没有其他的限定条件或说明时,卡方检验一般指代的是皮尔森卡方检验。在卡方检验的一般运用中,研究人员将观察量的值划分成若干互斥的分类,并且使用一套理论(或零假设)尝试去说明观察量的值落入不同分类的概率分布的模型。而卡方检验的目的就在于去衡量这个假设对观察结果所反映的程度。
在1900年,皮尔森发表了著名的关于\(\chi ^{2}\)检验的文章,该文章被认为是现代统计学的基石之一。在该文章中,皮尔森研究了拟合优度检验:
假设实验中从总体中随机取样得到的\(n\)个观察值被划分为\(k\)个互斥的分类,这样每个分类都有一个对应的实际观察次数\(x _ { i } ( i = 1,2 , \dots , k )\)。研究人员会对实验中各个观察值落入第\(i\)个分类的概率\(p_{i}\)的分布提出零假设,从而获得了对应所有第\(i\)分类的理论期望次数\(m_{i}=np_{i}\)以及限制条件\(\sum _{i=1}^{k}{p_{i}}=1\)以及\(\sum _{i=1}^{k}{m_{i}}=\sum _{i=1}^{k}{x_{i}}=n\)。
皮尔森提出,在上述零假设成立以及\(n\)趋向\(\infty\)的时候,以下统计量的极限分布趋近服从自由度为\((k-1)\)的卡方分布:
\[\chi _ { k - 1 } ^ {2} = \sum _ {i=1}^{k}{\frac {(x_{i}-m_{i})^{2}}{m_{i}}}\]其中\(x_i\)代表观察值频数,\(m_i\)代表期望值频数,当把观察值分为\(j\)组、\(k\)个互斥分配时,其自由度为\((j-1)(k-1)\),通常表示为分组表格的\((行数-1)\times(列数-1)\);
由卡方分布延伸出来皮尔森卡方检定常用于:
- 样本某性质的比例分布与总体理论分布的拟合优度(例如某行政机关男女比是否符合该机关所在城镇的男女比);
- 同一总体的两个随机变量是否独立(例如人的身高与交通违规的关联性);
- 二或多个总体同一属性的同素性检定(意大利面店和寿司店的营业额有没有差距)。
例如:一个六面骰子,抛1000000次,得到点数分布如下,是否可据此断定骰子的点数是均匀的?
| 点数 | 出现次数 |
|---|---|
| 1 | 166100 |
| 2 | 167100 |
| 3 | 166200 |
| 4 | 167300 |
| 5 | 166000 |
| 6 | 167300 |
这种已知理论分布,求实验数据拟合度的问题,可先假设其成立,然后用卡方检验判断。过程如下:
1.根据原假设,即均匀概率算出理论期望值: \(\overline { E } _ { 1 } = \overline { E } _ { 2 } = \overline { E } _ { 3 } = \overline { E } _ { 4 } = E _ { 5 } = \overline { E } _ { 6 } = 1000000 / 6 = 1666666.67\)
2.观察值\(x_i\)即是上表的数值,将其和理论值代入卡方值公式\(\chi _ { k - 1 } ^ {2} = \sum _ {i=1}^{k}{\frac {(x_{i}-m_{i})^{2}}{m_{i}}}\),算出卡方值\(\chi^2 = 11.84\)。
3.将卡方值代入\(k=6-1=5\)自由度的卡方分布,算出p值为0.03704715。结果表明这组数据的偏离程度仅优于大约4%的可能性,小于通常认为的5%,可以拒绝原假设。即这个骰子不能认为是均匀的。
例如,经过采样调查,男女对猫和狗的喜爱人数分别是下表格,则人们对宠物的喜爱是否与性别有关?
| 猫 | 狗 | |
|---|---|---|
| 男 | 207 | 282 |
| 女 | 231 | 242 |
解:这是一个检验随机变量是否独立的问题(性别与猫狗)。则这里建立零假设\(H_0\):性别与喜欢动物种类无关。
样本中男性总人数为\(207 + 282 = 489\),女性总人数为\(231 + 242 = 473\),总人数为\(489 + 473 = 962\)。
这根据\(H_0\)来计算男女对调查数据的理论值:
猫 狗 男 \(\frac {489 \times (207 + 231) } {962} = 222.64\) \(\frac {489 \times (282 + 242) } {962} = 266.36\) 女 \(\frac {473 \times (207 + 231) } {962} = 215.36\) \(\frac {473 \times (282 + 242) } {962} = 257.64\) 计算统计量: \(\chi ^ 2 = \frac {(207 - 222.64) ^ 2} {222.64} + \frac {(282 - 266.36) ^ 2} {266.36} + \frac {(231 - 215.36) ^ 2} {215.36} + \frac {(242 - 257.64) ^ 2} {257.64} = 4.102\)
\[自由度(DF) = (行数 − 1) 乘以 (列数 − 1) = (2 − 1)(2 − 1) = 1 \times 1 = 1\]查表得 p = 0.04283 < 0.05,故否定\(H_0\),认为对宠物的喜爱有性别关系。
F检验
F检验(F-test),最常用的别名叫做联合假设检验(英语:joint hypotheses test),此外也称方差比率检验、方差齐性检验。它是一种在零假设(null hypothesis, H0)之下,统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型,以判断该模型中的全部或一部分参数是否适合用来估计母体。
F检验通常来检验两组样本来自的各自独立总体是否均有相同的方差,因此常被称为方差比率检验、方差齐性检验。其要求两个被测试总体服从正态分布。其与t检查的区别是,t检验通过样本均值来检验两个总体的差异,其要求两个被测试总体具有相同的方差,满足方差齐性。因此在有些未给出方差齐性假设的场景时,需要先进行F检验。
有两个样本\(X = \left\{ x _ { 1 } , x _ { 2 } , \ldots , x _ { n } \right\}\)和\(Y = \left\{ y _ { 1 } , y _ { 2 } , \ldots , y _ { m } \right\}\)服从正态分布,则它们的均值可以表示为:
\[\begin{aligned} \overline { X } & = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } x _ { i } \\ \overline { Y } & = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } y _ { i } \end{aligned}\]我们可以计算得到它们对应的样本方差:
\[S _ { X } ^ { 2 } = \frac { 1 } { n - 1 } \sum _ { i = 1 } ^ { n } \left( x _ { i } - \overline { X } \right) ^ { 2 } \text { and } S _ { Y } ^ { 2 } = \frac { 1 } { m - 1 } \sum _ { i = 1 } ^ { m } \left( y _ { i } - \overline { Y } \right) ^ { 2 }\]则统计量\(F\)可以表示为:
\[F = \frac { S _ { X } ^ { 2 } } { S _ { Y } ^ { 2 } }\]在计算得到\(F\)后,我们可以查表得到的F表值比较(关于如何查询F表的方法在12中有所叙述),如果:
- \(F_{1-α/2} < F < F_{α/2}\) 表明两组数据没有显著差异(方差相等);
- \(F ≥ F_{α/2} 或 F ≤ F_{1-α/2}\) 表明两组数据存在显著差异。
\(F_{1-α/2}\)与\(F_{α/2}\)互为倒数,即\(F_{α/2} = \frac { 1 } { F_{1-α/2} }\),
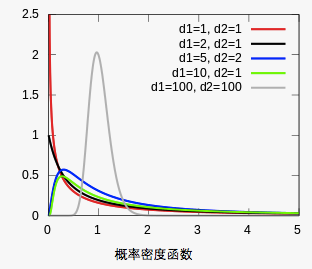
为了方便查F值表而不用计算倒数,在方差的齐性检验时,其检验公式为:
\[F = \frac { S _ { 大 } ^ { 2 } } { S _ { 小 } ^ { 2 } }\]例题:某区幼儿园对幼儿进行健康检查,从中随机抽取20名4岁幼儿,其中男生12名,女生8名,经计算得男生体重标准差为1.75公斤,女生体重的标准差为1.73公斤,试问该区4岁男女幼儿体重的方差差异是否显著。
解:建立假设:\(H _ { 0 } : S _ { 1 } ^ { 2 } = S _ { 2 } ^ { 2 }, H _ { 1 } : S _ { 1 } ^ { 2 } \neq S _ { 2 } ^ { 2 }\)
计算统计量:
\[\begin{array} { l } { S _ { n _ { 1 } - 1 } ^ { 2 } = \frac { n _ { 1 } } { n _ { 1 } - 1 } S _ { 1 } ^ { 2 } = \frac { 12 } { 11 } \times 1.75 ^ { 2 } = 3.34 } \\ { S _ { n _ { 2 } - 1 } ^ { 2 } = \frac { n _ { 2 } } { n _ { 2 } - 1 } S _ { 2 } ^ { 2 } = \frac { 8 } { 7 } \times 1.73 ^ { 2 } = 3.42 } \\ { F = \frac { S _ { n _ { 2 } - 1 } ^ { 2 } } { S _ { n _ { 1 } - 1 } ^ { 2 } } = \frac { 3.42 } { 3.34 } = 1.02 } \end{array}\]判断结果:
查F值得:\(F _ { ( 7,10 ) .05 / 2 } = 3.95 , F _ { ( 7,12 ) .05 / 2 } = 3.61\),
由内插法得:\(F _ { ( 7,10 ).05/2 } = 3.78 , \because 1.02 < 3.78, \therefore P > 0.05\)差异不显著。
总结
关于更多高级的假设检验的方法不在此介绍之列,上述经典比较已经足以应对日常工作需要,需要用到更多高级方法时,在进行研究介绍。阅读完本文后,可以在阅读《假设检验》4,其中有很多例题,可以用以巩固。