本文内容来源于《分布式存储系统可靠性-如何估算》、《分布式存储系统可靠性-系统估算示例》和《分布式存储系统可靠性-设计模式》三篇文章。增补相关注释和个人理解,修正了一些原文中的错误。
如何估算
存储系统的可靠性
常规情况下,我们一般使用多幅本技术来提高存储系统的可靠性,不论是结构化数据库存储(典型mysql)、文档型Nosql数据库存储(mongodb)或者是常规的blob存储系统(GFS、Hadoop)等。
数据几乎是企业的生命所在,那么如何去衡量较为正确得去衡量集群数据的可靠性?如何进行系统设计使得集群数据达到更高的可靠性,这是本文要解答的疑问。
数据丢失与copyset(复制组)
在999块磁盘3备份系统中,同时坏三块盘情况下的数据丢失概率?这个跟存储系统的设计息息相关。我们先考虑两个极端设计下的情况
设计一:把999块磁盘组成333块磁盘对。
在这种设计情况下,只有选中其中一个磁盘对才会发生数据丢失。这种设计中,丢失数据的概率为 \(p = \frac {333}{ C_ {999} ^ {3}} = 2 \times 10^{-6}\)。
设计二:数据随机打散到999盘中,极端情况下,随机一块盘上的逻辑数据的副本数据打散在在所有集群中的998块盘中。这种设计中,丢失数据的概率为 \(\frac { C_{999}^{3}}{ C_{999}^{3}} = 1\),也就是必然存在。
数据被切分为\(C_{999}^{3}\)份,随机损坏3块磁盘,必然有一份数据丢失。
通过这两种极端的例子,我们可以看到数据的丢失概率跟数据的打散程度息息相关,为了方便后续阅读,这里我们引入一个新的概念copyset(复制组)1。
CopySet:包含一个数据的所有副本数据的设备组合,比如一份数据写入1,2,3三块盘,那么{1,2,3}就是一个复制组。
9个磁盘的集群中,最小情况下的copyset的组合数为3,copysets = {1,2,3}、{4,5,6}、{7,8,9},即一份数据的写入只能选择其中一个复制组,那么只有 {1,2,3}、{4,5,6}或者{7,8,9} 同时坏的情况下才会出现数据丢失。即最小copyset数量为N/R。
系统中最大的copyset的数目为\(C_N^R\),其中R为副本数,N为磁盘的数量。在完全随机选择节点写入副本数据的情况下,系统中的copyset数目会达到最大值\(C_N^R\)。即任意选择R个磁盘都会发生一部分数据的三个副本都在这R个盘上。
磁盘数量N,副本为R的存储系统中,copyset数量S, N/R < S < C(N, R)
磁盘故障与存储系统可靠性估算
磁盘故障与柏松分布
在正式估算概率之前还需要科普下一个基础的概率学分布:柏松分布,wiki百科详见柏松分布。柏松分布主要描述在一个系统中随机事件发生的概率,譬如汽车站台的候客人数的概率,某个医院1个小时内出生N个新生儿的概率等等,更佳形象的可参见 阮一峰的《泊松分布和指数分布:10分钟教程》)。
\[P ( N ( t ) = n ) = \frac { ( \lambda t ) ^ { n } e ^ { - \lambda t } } { n ! } \tag{1}\]如上为泊松分布的公式。等号的左边,P 表示概率,N表示某种函数关系,t 表示时间,n 表示数量,λ 表示事件的频率。
举个栗子:1000块磁盘在1年内出现10块概率为\(P(N(365) = 10)\)[注:t的平均单位为天]。λ为1000块磁盘1天内发生故障磁盘的数量,按照google的统计,年故障率在8%,那么 λ = 1000 × 8% ÷ 365 。
如上只是损坏N块磁盘的概率统计,那么怎么利用这个信息计算分布式系统中数据的可靠性(即数据丢失概率)的近似估算。
这里采用的是比较陈旧泊松分布公式形式,也可以参考2,得出的结果是一致的。
分布式存储系统中的丢失率估算
T时间内故障率
分布式存储存储系统中如何进行年故障率估算,我们先假定一种情况,T(1年时间内),系统存满数据的情况下,坏盘不处理。这种情况下统计下数据的年故障率。
这里我们先定义一些数据
N: 磁盘数量
T: 统计时间
K: 坏盘数量
S: 系统中copyset数量(复制组的个数)
R: 备份数量
如何计算T(1年)时间内数据丢失的概率,从概率统计角度来说就是把T(1年)时间内所有可能出现数据丢失的事件全部考虑进去。包含N个磁盘R副本冗余的系统中,在T时间内可能出现数据丢失数据的事件为坏盘大于等于R的事件,即R,R+1,R+2,… N (即为 K∈[R,N] 区间所有的时间),这些随机事件发生时,什么情况下会造成数据丢失?没错就是命中复制组的情况。
K个损坏情况下(随机选择K个盘情况下)命中复制组的概率为:
\[p(K) = \frac {X}{C_N^K} = \frac { \sum _ {i=1}^{ \lfloor \frac {K} {R} \rfloor } { C_{S}^{i} \times C_{(N - i \times R)} ^ {(K - i \times R)} } }{C_N^K} \tag{2}\]其中X为随机选择K个磁盘过程中命中复制组的组合数。那么系统出现K个磁盘损坏造成数据丢失的概率为:
\[Pa(T,K) = p(K) \times P(N(T)=K) \tag{3}\]最后系统中T时间内出现数据丢失的概率为所有可能出现数据丢失的事件的概率加起来:
\[Pb(T) = \sum _ {K=R} ^ {N} { Pa(T,K) } \tag{4}\]分布式系统衡量年故障率
以上我们假设在一年中,不对任何硬件故障做恢复措施,那么T用1年代入即可算出此种系统状态下的年故障率。但是在大规模存储系统中,数据丢失情况下往往会启动恢复程序,恢复完了之后理论上又是从初始状态的随机事件,加入这个因素之后计算可靠性会变得比较复杂。
理论上大规模存储系统中坏盘、恢复是极其复杂的连续事件,这里我们把这个概率模型简化为不同个单位时间T内的离散事件进行统计计算。只要两个T之间连续事件的发生概率极小,并且T时间内绝大部份坏盘情况能够恢复在T时间内恢复,那么下个时间T能就是重新从新的状态开始,则这种估算能够保证近似正确性。T的单位定义为小时(即),那么1年可以划分为\(\frac {365 \times 24} {T}\)个时间段,那么系统的年故障率可以理解为100%减去所有单位T时间内都不发生故障的概率。即系统整体丢失数据的概率为:
\[Pc = 1 - (1-Pb(T)) ^ {\frac {365 \times 24} {T}} \tag{5}\]系统估算示例
估算示例
上面我们提供了一些基本的估算的方法。接下来我们提供一个具体的估算的示例子。
系统示例: N = 7200块磁盘的存储系统中,R=3副本,单盘容量 DiskSize = 8T,磁盘年平均故障率 AFR = 4%,系统采用大多数存储系统采用的小文件合并成大文件分片的方式存储,分片大小为 PartSize = 10GB,系统整体空间利用率 Percent = 70%(系统总体承载数据量大约在13PB),分片采用随机放置方式,随机放置情况下 \(S = Min( C_N^R, \frac {N \times DiskSize \times Percent} {R \times PartSize })\)。
上面
PartSize应该是分片数据不超过10GB,因为在Copysets理论1中,追求的是最小的S,则S越小,对应的分片大小PartSize越大,但是分片大小PartSize不是越大越好,通常处于查询效率等考虑,进行上限的约束。
以下为计算恢复时间T = 1小时情况下的概率的过程:
\(S = Min(C_{7200}^{3}, \frac {7200 \times 8 \times 1024 \times 70\% }{3 \times 10 } ) = 1376256\\ Pa(T,K) = P(1,K) = \frac {X} {C_{7200}^K} \times P( N(1) = K)\\ \lambda = \frac { 4\% \times 7200} { 365 \times 24 } = 0.03\\ P(N(1) = K) = \frac {\lambda ^ K e ^ {-\lambda}} {K!}\\ Pb(T) = \sum _ {i=3} ^ {7200} {P(1,K)}\\ Pc = 1 - (1-Pb(T)) ^ {(365*24/1)}\)
(按照4%的坏盘率计算7200块盘的系统中平均每小时的坏盘数量)
可以看到其中 选K个节点情况下,命中copyset的概率为\(\frac {X}{C_{7200}^K}\)。 这个X的计算我们暂时还没有确定,我们看下这个如何计算。K = 3的情况下,即\(Pa(1,3) = \frac {S}{C_{7200}^{3}} \times P(N(1) = 3)\)比较简单,但是在K∈[4, 7200]点情况下,情况就比较复杂了,貌似没有一种比较好的统一的组合概率计算这个概率。如果非要计算基本可以使用蒙特卡罗方法case by case 进行计算,该方法详见附录。如果我们在分析概率的基础上进行进一步简化估算。
通过计算P(N(1),K) 可以计算得到1小时内坏K个的概率:
| K | P(N(1), K) | P(1,K) |
|---|---|---|
| 3 | 5.73e-6 | 1.26e-10 |
| 4 | 4.71e-8 | ? |
| 5 | 3.09e-10 | ? |
| 6 | 1.69e-12 | ? |
| 7 | 7.97e-15 | ? |
| 8 | 3.27e-17 | ? |
| 9 | 1.19e-19 | ? |
从上面我们可以看到,在K>=6情况下,假设选中copyset的概率为1,对结果的影响也是比K=3小2个数量级以上。所以基本只需要统计考虑K=4、K=5情况下的即可。K=4,5 情况下的选中CopySet的概率基本为\(\frac {C_S^1 \times C_{N-3}^{K-3}} {C_N^K}\)。
| K | P(N(1),K) | P(1,K) |
|---|---|---|
| 3 | 5.73e-6 | 1.26e-10 |
| 4 | 4.71e-8 | 4.17e-12 |
| 5 | 3.09e-10 | 6.85e-14 |
此处可以类比傅里叶级数展开,高次项对整体量纲的贡献非常低,在粗略计算时往往可以省略。
\(Pb(T) \approx \sum _ {3}^{5}{P(1,K)} = 1.31 \times 10 ^ {-10}\) (即T=1小时内 丢数据的概率为1.31e-10)
\(Pc = 1 - (1-Pb(T))^{\frac {365 \times 24}{T}} = 1.1 \times 10 ^{-06}\), 即6个9的可靠性。
估算代码:
这里有一份学习后,使用golang实现的
#!/usr/bin/python
# -*- coding: utf-8 -*-
import decimal
import math
import time
# 随机分布情况下系统的copyset组合数
def RandomCopySets(N, DiskSize, RepNum, Percent, PartSize):
setNum = (N * DiskSize * Percent / (RepNum * PartSize))
MaxCopySetNum = C(N, RepNum)
copysetNum = 0
if setNum > MaxCopySetNum:
copysetNum = MaxCopySetNum
else:
copysetNum = setNum
return int(copysetNum)
# N 个磁盘存储系统中T时间同时损坏K块盘的概率,年故障率ARF
def KdiskFailRate(N, T, ARF, K):
# λ 每小时的换盘数量
lambda1 = decimal.Decimal(str(N*AFR/24/365))
return poisson(lambda1, T, K)
# 副本数R的N 个磁盘存储系统中T时间内造成数据丢失的概率, 只统计R -> 2R-1个副本情况下的丢失数据概率(大于R个情况下,在一遍情况下对结果影响比较小)
def LossDataInT(S, N, RepNum, T, ARF):
loosRate = decimal.Decimal(str(0.0))
for k in range(RepNum, RepNum*2):
kdrate = KdiskFailRate(N,T,ARF,k)
singlerate = S * C(N-3, k-3)/C(N,k)
kdlossrate = kdrate * singlerate
print "k = " + str(k) + ", " +str(kdrate) + ", " + str(kdlossrate)
loosRate += kdlossrate
print loosRate
return loosRate
# define loseRate in one Year
def LoseRate(S, N, RepNum, T, AFR):
return 1 - (1 - LossDataInT(S, N, RepNum, T, AFR))**(365*24/T)
#组合运算
def C(n, m):
return factorial(n) / (factorial(m)*factorial(n-m))
#泊松分布
def poisson(lam, t, R):
e=decimal.Decimal(str(math.e))
return ((lam * t) ** R) * (e**(-lam*t)) / factorial(R)
#t时间内损坏R块磁盘的概率
def probability(t, R):
return poisson(t, R)
#级数
def factorial(n):
S = decimal.Decimal("1")
for i in range(1, n+1):
N = decimal.Decimal(str(i))
S = S*N
return S
# case 1
N = 7200
DiskSize = 8*1024
Percent = 0.7
PartSize = 10
RepNum = 3
T = 1
AFR = 0.04
S = RandomCopySets(N, DiskSize, RepNum, Percent, PartSize)
print LoseRate(S, N, RepNum, T, AFR)
设计模式
从上文中详细分析了系统可靠性量化的估算手段,并且给出了示例代码,代码的主要输入参数为如下所示。
LoseRate(S, N, RepNum, T, AFR)
N: 系统中磁盘的数量(包括磁盘的容量信息)
S: 系统Copyset的数量
RepNum: 存储的备份数量
T: 坏盘情况下的恢复时间
AFR: 磁盘的年度故障率
这里基本可以揭示,在一个固定大小为N的分布式存储系统中,影响存储可靠性的因素主要为S、RepNum、T、AFR。接下来我们分别从这几个方面来分析,在分布式系统设计和运维过程中的一注意点。
年故障率(AFR)
排除人为因素和系统Bug,丢数据的核心原因是磁盘发生不可逆故障造成的。当前磁盘的过保时间大概是4年,4年后磁盘的故障率会急剧上升,同样从成本上考虑,随着磁盘技术的不断提升,存储密度每4年可以有很大得上升,替换使用新的磁盘更佳具备成本优势。如继续让老的磁盘在线上提供服务,系统丢失数据的风险会变大。根据google的生产环境的数据显示,磁盘的AFR数据如下:
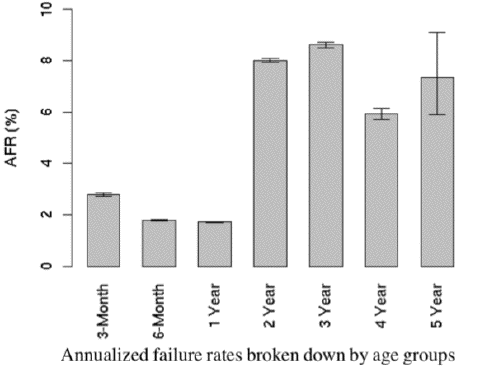
针对这一特性,我们潜在能够采取的措施包括:
- 及时替换老的或者故障磁盘
在系统设计层面上需要能够记录每一块硬盘的品牌、系列、上线日期等,对于经常出现坏块和频繁出错的磁盘需要尽快进行,并且对于快要使用年限的磁盘进行替换下线。
- 根据SMART信息预测换盘
采集磁盘的SMART的信息,分析SMART信息,对磁盘的换盘行为做预测工作。
副本数(RepNum)
显然副本数是影响数据可靠性的关键因素。这里我们通过量化的方式来衡量副本数对可靠性的影响。
使用的系统示例分布式存储系统可靠性-系统估算示例。考虑副本数 R∈[3,6] 情况下的可用性,如下所示:
| RepNum | 可靠性(年故障率) |
|---|---|
| 3 | 1.14*10E-6 |
| 4 | 2.78*10E-8 |
| 5 | 3.18*10E-10 |
| 6 | 3.32*10E-12 |
| 7 | 2.33*10E-14 |
从上表可以看出,增加副本可以使得可靠性得到数量级上的提升,但是成本和写入性能上会给系统带来一定的负担。产品可以从数据的重要性,系统本身的workload等方面在在各方面权衡选择系统的副本数。
Copyset数目(S)
单从copyset 这一因素考虑,我们基本可以确定CopySet越多丢数据概率会愈大,这我们可以从分布式存储系统可靠性-如何估算文中第2节数据丢失与copyset(复制组)看出。
以下,我们同样以Copyset与丢失数据概率具体看CopySet对可靠性的影响,使用系统示例同样为分布式存储系统可靠性-系统估算示例中的示例,随机情况下CopySet数量为S
| CopySetsNum | 可靠性(年故障率) |
|---|---|
| S | 1.14*10E-6 |
| S/2 | 5.74*10E-7 |
| S/4 | 2.87*10E-7 |
| S/8 | 1.43*10E-7 |
| S/16 | 7.17*10E-8 |
从上表我们可以看到,减小copyset数量对于可靠性的影响基本是线性。
那么如何规划系统中copyset的数量。在随机策略情况下,copyset的数量越多,说明一个磁盘上的数据打得越散,那么一块磁盘上对应的数据的副本分布在更多的磁盘上,可以获得更高的恢复带宽,坏盘的恢复时间越短,从而进一步降低丢失数据的风险。但是在现实系统中,为了保障数据对外服务的带宽能力。一般来说用于系统恢复的带宽不会超过20%,所以T级别盘能够在1个小时内恢复已经是非常不错的。
比如一块8T盘1小时恢复所需要的带宽8 * 1024 / 3600 ≈ 2.27 GB,假设每块磁盘能够提供的恢复带宽为10MB,那么只需要 2.27 * 1024 / 20 ≈ 106块盘参与即可,也就是说一块磁盘的数据只需要打散在106块磁盘中即可,不用过于分散。在随机放置副本情况下,我们可以控制分片大小来达到减小copyset的目的分片大小 ≈ 8 * 1024 / 106 = 77GB。 这种清下,可靠性可以提高到1.49*10E-7 。 后续我们会介绍更佳有效的控制系统copyset的方法。
修复时间(T)
单从修复时间考虑,修复时间越快,丢失概率越小。因为同时发生坏盘的概率随着时间的缩短能够得到非常有效的降低。这从分布式存储系统可靠性-如何估算中介绍坏盘服从的柏松分布中可以看到。
如下为N=7200,AFR=0.04情况下;在单位时间[1,24]内坏[3~6]块盘的概率;从图表中我们可以看到,从20小时变为2小时,时间段内损坏N块盘(3~6)的概率都能得到3个数量级以上的提升。
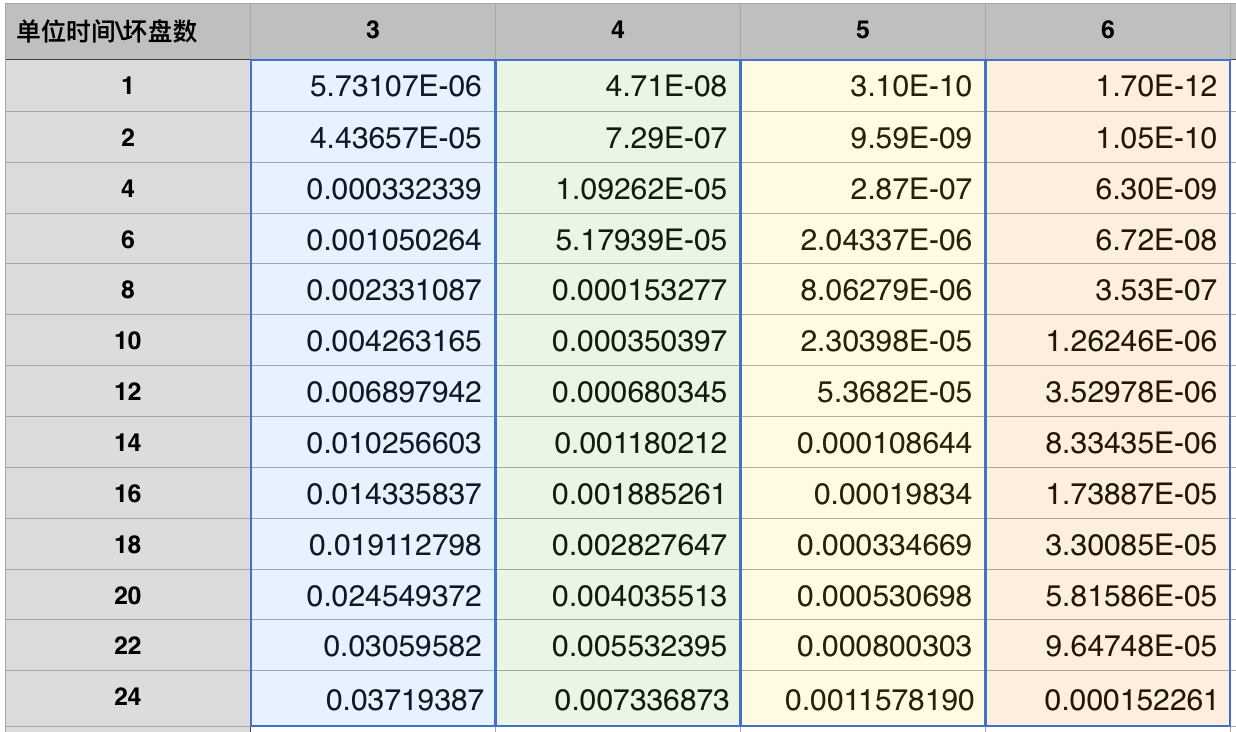
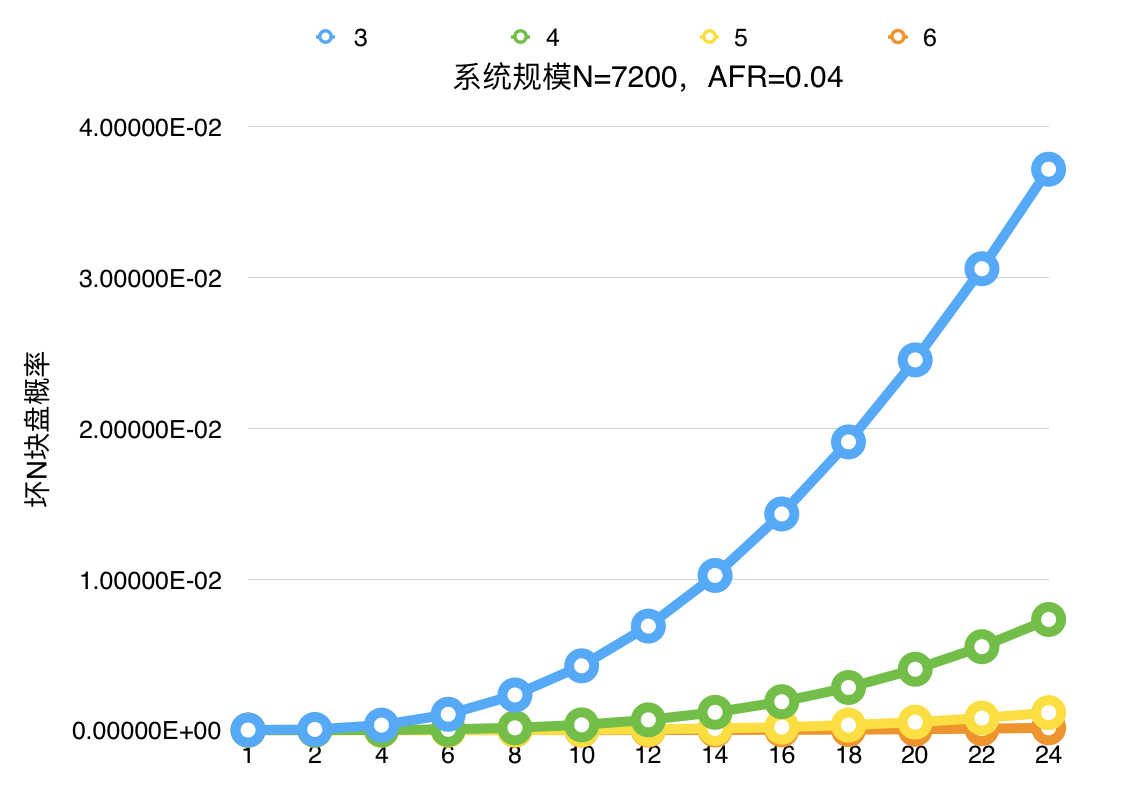
总结
总结来说,为了提高存储系统数据可靠性,首先在系统允许的成本范围内选择合适的副本数,再次在系统设计中我们首先优先考虑加快数据恢复时间,在此基础上减小系统的copyset数量。使得在既定的成本下达到尽可能高的可靠性。
参考
文档信息
- 本文作者:Neal Hu
- 本文链接:https://lrita.github.io/2019/01/30/distributed-system-reliable/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)